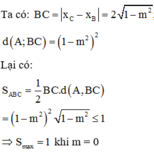Tìm m để hàm số y= (m2 +1)x4 -2(m4+1)x2 +3-m có giá trị cực đại bằng 2
Những câu hỏi liên quan
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất các giá trị của tham số m để hàm số cực đại, cực tiểu và các điểm cực trị của đồ thị lập thành một tam giác có diện tích lớn nhất A.
m
1
2...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất các giá trị của tham số m để hàm số cực đại, cực tiểu và các điểm cực trị của đồ thị lập thành một tam giác có diện tích lớn nhất
A. m = 1 2
B. m = 0
C. m = 1
D. m = - 1 2
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số m để hàm số có...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = 0
B. m = - 1 2
C. m = 1
D. m = 1 2
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có 
R
Phương trình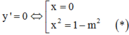 
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác 
Khi đó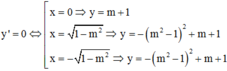 
Gọi 
; 
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là 
Và 
Diện tích tam giác ABC là 
Mà 
R suy ra 
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số thực m để hàm...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = - 1 2
B. m = 1 2
C. m = 0
D. m = 1
Chọn C
[Phương pháp tự luận]
Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
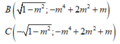
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
Vậy S đạt giá trị lớn nhất ⇔ m = 0
Đúng 0
Bình luận (0)
Cho hàm số yx4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất. A. m -1/2 B. m 1/2 C. m2 D. m1
Đọc tiếp
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Ta có
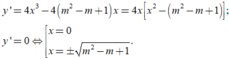
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó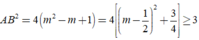 
Dấu xảy ra khi m=1/2.
Chọn B.
Đúng 0
Bình luận (0)
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Cho hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
2
.
Tìm m để hàm số có 3 điểm cực trị là 3 đỉnh của 1 tam giác vuông A. m 0 B. m 1 C. m -1 D. m 2
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m - 1 ) x 2 + m 2 . Tìm m để hàm số có 3 điểm cực trị là 3 đỉnh của 1 tam giác vuông
A. m = 0
B. m = 1
C. m = -1
D. m = 2
Với giá trị nào của tham số m thì đồ thị hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
4
-
3
m
2
+
2017
có 3 điểm cực trị tạo thành 1 tam giác có diện tích bằng 32? A. m 2 B. m 3 C. m 4 D. m 5
Đọc tiếp
Với giá trị nào của tham số m thì đồ thị hàm số y = x 4 - 2 ( m - 1 ) x 2 + m 4 - 3 m 2 + 2017 có 3 điểm cực trị tạo thành 1 tam giác có diện tích bằng 32?
A. m= 2
B. m= 3
C. m= 4
D. m= 5
Tìm tất cả các giá trị của m để đồ thị hàm số y
(
m
2
-
1
)
x
4
+
m
x
2
+
m
-
2
chỉ có một điểm cực đại và không có điểm cực tiểu. A. -1,5 m
≤
0 B. m
≤
1 C. -1
≤
m
≤...
Đọc tiếp
Tìm tất cả các giá trị của m để đồ thị hàm số y = ( m 2 - 1 ) x 4 + m x 2 + m - 2 chỉ có một điểm cực đại và không có điểm cực tiểu.
A. -1,5 < m ≤ 0
B. m ≤ 1
C. -1 ≤ m ≤ 0
D. -1 < m < 0,5
Chọn C.
Tập xác định: D = ℝ
Xét 
Với m = 1, hàm số đã cho trở thành: 
Hàm số này đạt cực tiểu tại điểm A(0;-1) nên không thỏa mãn yêu cầu bài toán.
Với m = -1, hàm số đã cho trở thành: 
Hàm số này đạt cực đại tại điểm B(0;-3) nên thỏa mãn yêu cầu bài toán.
Xét m
≠
±
1 ta có 
Xét y' = 0 
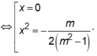
Với m = 0 phương trình y' = 0 có nghiệm bồi 3 và 
nên hàm số đạt cực đại tại điểm C(0;-1) nên thỏa mãn yêu cầu bào toán.
Với m ≠ 0 hàm số đã cho chỉ có một điểm cực đại và không có điểm cực tiểu khi và chỉ khi
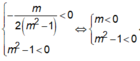
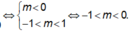
Đúng 0
Bình luận (0)
Với giá trị nào của tham số m thì đồ thị hàm số
y
x
4
-
2
(
m
-
1
)
x
2
+
m
4
-
3
m
2
+
2017
có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 32 A.m4 B.m5 C.m3 D.m2
Đọc tiếp
Với giá trị nào của tham số m thì đồ thị hàm số y = x 4 - 2 ( m - 1 ) x 2 + m 4 - 3 m 2 + 2017 có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 32
A.m=4
B.m=5
C.m=3
D.m=2
