Tìm GTNN và GTLN của hàm số:
y=4sin2x−4sinx+
Tìm GTNN,GTLN của y=4sin2x -3sinx -1
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=4t^2-3t-1\)
Xét hàm \(f\left(t\right)\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{3}{8}\in\left[-1;1\right]\)
\(f\left(-1\right)=6\) ; \(f\left(\dfrac{3}{8}\right)=-\dfrac{25}{16}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{25}{16}\) khi \(sinx=\dfrac{3}{8}\)
\(y_{max}=6\) khi \(sinx=-1\)
Tìm GTNN,GTLN của y=3 -4sinx
\(sin\in\left[-1;1\right]\Rightarrow y=3-4sinx\in\left[-1;7\right]\)
\(\Rightarrow y_{min}=-1\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=7\Leftrightarrow sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)
Tìm GTLN và GTNN của hàm số y = √3cosx - sinx
\(y=\sqrt{3}cosx-sinx=2\left(\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\right)=2cos\left(x+\dfrac{\pi}{6}\right)\)
Vì \(cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{3}cosx-sinx\in\left[-2;2\right]\)
\(\Rightarrow y_{min}=-2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=-1\Leftrightarrow x+\dfrac{\pi}{6}=\pi+k2\pi\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
\(y_{max}=2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=1\Leftrightarrow x+\dfrac{\pi}{6}=k2\pi\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\)
Tìm GTLN và GTNN của hàm số: y = |sinx + cos2x|
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)
Tìm GTLN và GTNN của hàm số y = 3 + sin2x
21.
a) `2sin(x-30^@)-1=0`
`<=>sin(x-30^@)=1/2`
`<=> sin(x-30^@)=sin30^@`
`<=>[(x-30^@=30^@+k360^@),(x-30^@=180^@-30^@+k360^@):}`
`<=> [(x=60^@+k360^@),(x=180^@+k360^@):}`
b) `5sin^2x+3cosx+3=0`
`<=>5(1-cos^2x)+3cosx+3=0`
`<=>-5cos^2x+3cosx+8=0`
`<=>(cosx+1)(cosx=8/5)=0`
`<=>[(cosx=-1),(cosx=8/5\ (VN)):}`
`<=>x=180^@+k360^@`
22.
`-1<=sin2x<=1`
`<=>2<=3+sin2x<=4`
`=> y_(min)=2 ; y_(max)=4`
Tìm GTLN và GTNN của hàm số
y=3sinx + 4cosx + 5
A. min y = 0, max y= 13
B. min y =0, max y=10
C. min y= 1, max y=10
D. Tất cả sai
Tìm GTLN và GTNN của hàm số sau: y = 1 - 2 cos 2 x + 1
![]()
![]()
![]()
![]()
Tìm GTLN và GTNN của hàm số: y = 2 sin x + cos x + 3 2 cos x - sin x + 4
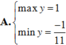
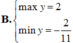
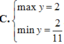
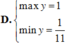
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
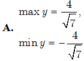
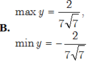


Tìm GTLN, GTNN của hàm số sau
a) y = 12sinx - 5cosx
b) y = 3cosx-4sinx+5
a) Ta có : -\(\sqrt{a^2+b^2}< =asinx+bcosx< =\sqrt{a^2+b^2}\)
=> \(-\sqrt{12^2+\left(-5\right)^2}< =y< =\sqrt{12^2+\left(-5\right)^2}\)
<=> \(-\sqrt{13}< =y< =\sqrt{13}\)
Vậy min=\(-\sqrt{13}\) ,max=\(\sqrt{13}\)
b) \(-\sqrt{9+16}< =3cosx-4sinx< =\sqrt{9+16}\)
<=> -5 <=3cos x -4sinx <= 5
<=> 0<= y <= 10
Vậy min=0 max=10