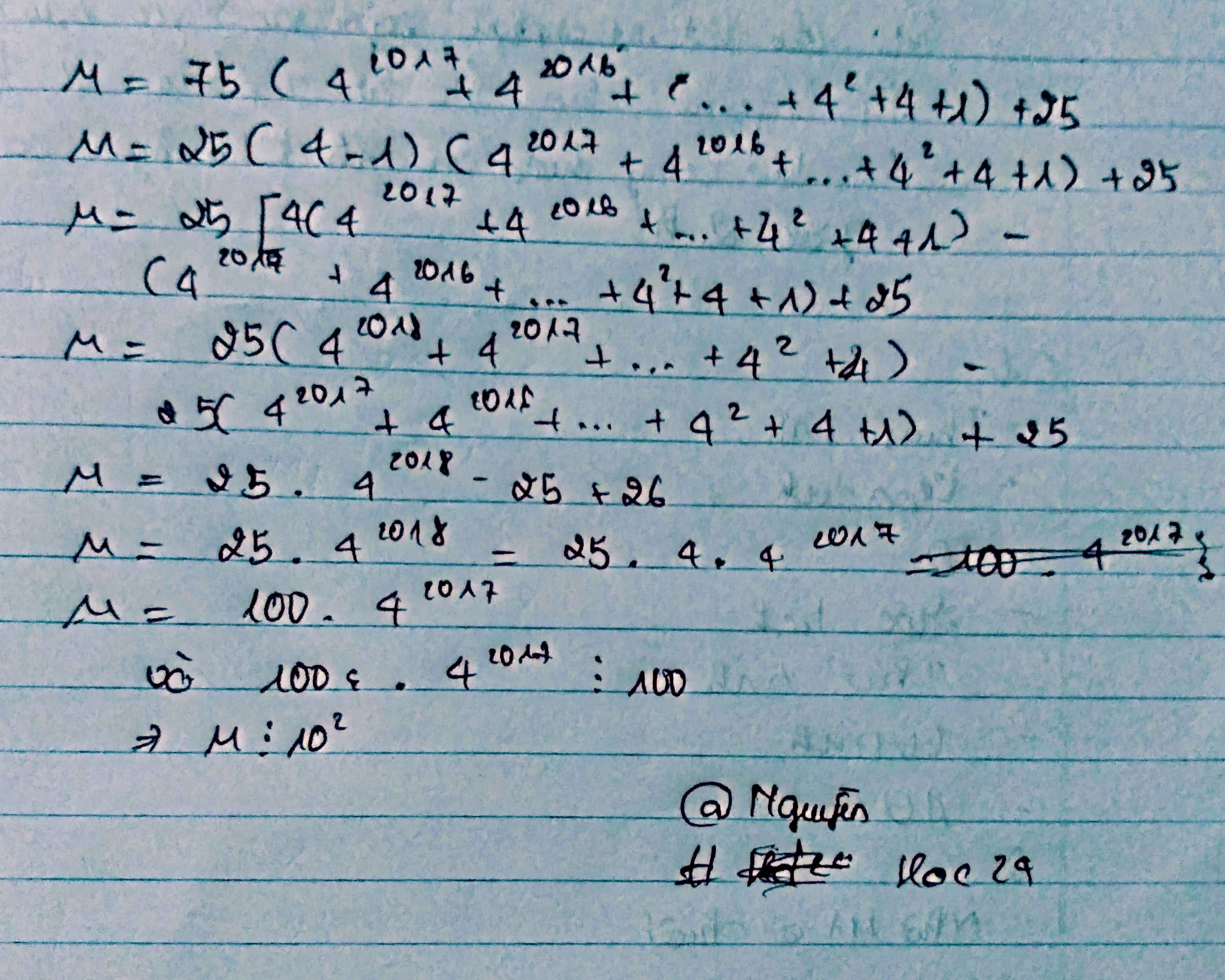CMR biểu thức A=75.(4^2017+4^2016+..+4^2+5)+25 chia hết cho 4^2018

Những câu hỏi liên quan
Cho biểu thức B = 75 ( 1 + 4 +42 + .....+ 42017 + 42018 ) +25
CMR B chia hết cho 400
Tìm tất cả các chữ số a,b,c thỏa mãn
abc-cba=6b3
Tìm một số chính phương có 3 chữ số biết rằng nó chia hết cho 56
CMR: A=75(42018+42017+....+42+5)+25 chia hết cho 42019
CÁC BẠN GIÚP MÌNH NHA !
A = 75 . (40 + 41 + 42 + ..... + 42017 + 42018) + 25
a, CMR : A chia hết cho 100
b, CMR : A chia hết cho 3
c, Tìm 2 chữ số tận cùng của A
Theo tính chất đề bài ta có: Achia hết 100
Đúng 0
Bình luận (0)
cậu có thể giải thich rõ hơn được không?
Đúng 0
Bình luận (0)
C = 75 . ( $4^{2019}$ + $4^{2018}$ + $4^{2017}$ + ... + $4^{2}$ + 4 +1 ) + 25
Chứng tỏ C chia hết cho 100
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)
Đúng 0
Bình luận (0)
Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102
cho A =1+2^2018+3^2017+4^2016+...+2018^2+2019,B=1+2^2017+3^2016+...+2017^2+2018,chứng tỏ giá trị biểu thức A-3B dương
cho A =1+2^2018+3^2017+4^2016+...+2018^2+2019,B=1+2^2017+3^2016+...+2017^2+2018,chứng tỏ giá trị biểu thức A-3B dương
Cho biểu thức B=75+(1+4+\(4^2\)+...+\(4^{2018}\))+25. Chứng minh rằng B chia hết cho 400
1) Cmr : \(A=75\left(4^{2015}+4^{2014}+4^{2013}+....+4^2+5\right)+25\)chia hết cho \(4^{2016}\)
đặt B = 42015 + 42014 + 42013 + ... + 42
4B = 42016 + 42015 + 42014 + ... + 43
4B - B = ( 42016 + 42015 + 42014 + ... + 43 ) - ( 42015 + 42014 + 42013 + ... + 42 )
3B = 42016 - 42
\(\Rightarrow\)B = \(\frac{4^{2016}-4^2}{3}\)hay B = \(\frac{4^{2016}-16}{3}\)
\(\Rightarrow\)A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ 5 ) + 25
A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ \(\frac{15}{3}\)) + 25
A = 75 . ( \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 3 . \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 42016 - 1 ) + 25
A = 25 . ( 42016 - 1 + 1 )
A = 25 . 42016 \(⋮\)42016
Đúng 0
Bình luận (0)