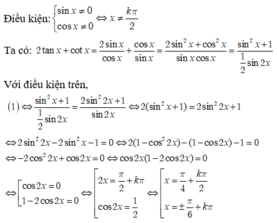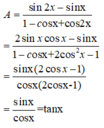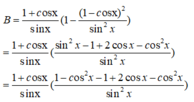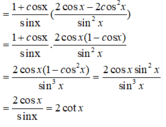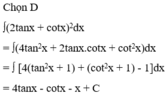\(2tanx+cotx=2sin2x+\frac{1}{sin2x}\)

Những câu hỏi liên quan
bài 1: giải pt
a,\(\frac{cos\left(cos+2sinx\right)+3sinx\left(sinx+\sqrt{2}\right)}{sin2x-1}=1\)
b,\(\frac{sin^22x-2}{sin^22x-4cos^2x}=tan^2x\)
c, \(\frac{1+sin2x+cos2x}{1+cot^2x}=\sqrt{2}sinxsin2x\)
d, \(2tanx+cotx=2sin2x+\frac{1}{sin2x}\)
Giải phương trình sau: 2tanx + cotx 2sin2x +
1
sin
2
x
A. B. C. D.
Đọc tiếp
Giải phương trình sau: 2tanx + cotx = 2sin2x + 1 sin 2 x
A. ![]()
B. ![]()
C. ![]()
D. 
Rút gọn các biểu thức sau:
A
sin
2
x
-
sin
x
1
-
c
o
t
x
+
cos
2
x
B
1
+
cos
x
sin
x
(
1...
Đọc tiếp
Rút gọn các biểu thức sau:
A = sin 2 x - sin x 1 - c o t x + cos 2 x B = 1 + cos x sin x ( 1 - ( 1 - cos x ) 2 sin 2 x )
Giải phương trình:
\(\dfrac{\sqrt{3}}{Cos^2x}+\dfrac{4+2Sin2x}{Sin2x}-2\sqrt{3}=2\left(Cotx+1\right)\)
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{\sqrt{3}}{cos^2x}+2+\dfrac{2}{sinx.cosx}-2\sqrt{3}=2\left(\dfrac{1}{tanx}+1\right)\)
\(\Leftrightarrow\sqrt{3}\left(1+tan^2x\right)+\dfrac{\dfrac{2}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}}+2-2\sqrt{3}=2\left(\dfrac{1}{tanx}+1\right)\)
\(\Leftrightarrow\sqrt{3}tan^2x+\dfrac{2\left(1+tan^2x\right)}{tanx}+2-\sqrt{3}=\dfrac{2}{tanx}+2\)
\(\Leftrightarrow\sqrt{3}tan^3x+2\left(1+tan^2x\right)-\sqrt{3}tanx=2\)
\(\Leftrightarrow\sqrt{3}tan^3x+2tan^2x-\sqrt{3}tanx=0\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
chứng minh rằng :\(\frac{2tanx-sin2x}{\left(sinx+cosx\right)^2-1}=tan^2x\)
Giả sử biểu thức xác định
\(\frac{2tanx-sin2x}{\left(sinx+cosx\right)^2-1}=\frac{2tanx-sin2x}{sin^2x+cos^2x+2sinx.cosx-1}=\frac{2tanx-2sinx.cosx}{2sinx.cosx}\)
\(=\frac{sinx}{cosx.sinx.cosx}-1=\frac{1}{cos^2x}-1=\frac{1-cos^2x}{cos^2x}=\frac{sin^2x}{cos^2x}=tan^2x\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a,\(\dfrac{sin2x+cosx-\sqrt{3}\left(cos2x+sinx\right)}{2sin2x-\sqrt{3}}\)
=1
b,
(2cosx-1)cotx=\(\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\)
a.\(\dfrac{sin2x+cosx-\sqrt{3}\left(cos2x+sinx\right)}{2sin2x-\sqrt{3}}=1\left(1\right)\)
ĐKXĐ: sin2x≠\(\dfrac{\sqrt{3}}{2}\)
(1) ⇔ sin2x + cosx - \(\sqrt{3}\) ( cos2x + sinx) = 2sin2x - \(\sqrt{3}\)
⇔cosx - \(\sqrt{3}\) sinx = \(\sqrt{3}\) cos2x + sin2x +\(\sqrt{3}\)
⇔\(\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=sin\left(2x+\dfrac{\Pi}{3}\right)-sin\dfrac{\Pi}{3}\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=2cos\left(x+\dfrac{\Pi}{3}\right)sinx\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=2sin\left(\dfrac{\Pi}{6}-x\right)sinx\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)\left(2sinx-1\right)=0\)
Đến đây tự giải tiếp nha nhớ đối chiếu đk.
Đúng 0
Bình luận (0)
b.\(\left(2cosx-1\right)cotx=\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\left(1\right)\)
ĐKXĐ: sinx≠0 và cosx≠1
(1)⇔\(\left(2cosx-1\right)\dfrac{cosx}{sinx}=\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\)
⇔cosx(2cosx-1)(cosx-1) = 3(cosx-1) + 2sin2x
⇔2cos3x - cos2x - 2cosx +1 = 0
⇔ (cosx-1)(cosx+1)(2cosx-1)=0
Đúng 0
Bình luận (0)
\(cotx-1=\frac{cos2x}{1+tanx}+sin^2x-\frac{1}{2}sin2x\)
ĐKXĐ: \(\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne-1\end{matrix}\right.\)
\(\frac{cosx}{sinx}-1=\frac{cos^2x-sin^2x}{1+\frac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\frac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\Rightarrow x=\frac{\pi}{4}+k\pi\\\frac{1}{sinx}=cosx-sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sinx.cosx-sin^2x=1\)
\(\Leftrightarrow2sinx.cosx+1-2sin^2x=3\)
\(\Leftrightarrow sin2x+cos2x=3\)
Vế trái không lớn hơn 2 nên pt vô nghiệm
Đúng 0
Bình luận (0)
chứng minh rằng
1) \(\frac{sin2x}{1+cos2x}=cotx\)
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}\)
\(=\frac{sinx}{cosx}=tanx\)
Đề bài sai, kết quả ra tan chứ ko phải cot
Đúng 0
Bình luận (0)
Họ nguyên hàm của hàm số f ( x ) = ( 2 t a n x + c o t x ) 2 là:
A. 2tanx - cotx - x + C
B. 4tanx + cotx - x + C
C. 4tanx - cotx + x + C
D. 4tanx - cotx - x + C