Phân tích đa thức sau thành nhân tử
a) x2y + xy2 + x + 1
b)x2 - (a+b).x + ab
c) x2y + xy2 - x - y
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:a) 4
(
2
-
x
)
2
+ xy - 2y;b) x
(
x
-
y
)
3
-
y
(
y
-
...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) 4 ( 2 - x ) 2 + xy - 2y;
b) x ( x - y ) 3 - y ( y - x ) 2 - y 2 (x - y);
c) x 2 y - xy 2 - 3x + 3y;
d) x ( x + y ) 2 - y ( x + y ) 2 + xy - x 2
phân tích đa thức thành nhân tử
a)70a+84b-20ab-24b2
b) x2y+xy2+x2z+xz2+y2z+yz2+3xyz
c) x2y+xy2+x2z+xz2+y2z+yz2+2xyz
a) \(70a+84b-20ab-24b^2\)
\(=\left(70a+84b\right)-\left(20ab+24b^2\right)\)
\(=14\left(5a+6b\right)-4b\left(5a+6b\right)\)
\(=\left(5a+6b\right)\left(14-4b\right)\)
\(=2\left(5a+6b\right)\left(7-2b\right)\)
b) \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)
\(=\left(x^2y+xy^2+xyz\right)+\left(x^2z+xyz+xz^2\right)+\left(xyz+y^2z+yz^2\right)\)
\(=xy\left(x+y+z\right)+xz\left(x+y+z\right)+yz\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)
c) \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+2xyz\)
\(=\left(x^2y+xy^2\right)+\left(xz^2+yz^2\right)+\left(x^2z+2xyz+y^2z\right)\)
\(=xy\left(x+y\right)+z^2\left(x+y\right)+z\left(x^2+2xy+y^2\right)\)
\(=xy\left(x+y\right)+z^2\left(x+y\right)+z\left(x+y\right)^2\)
\(=\left(x+y\right)\left[xy+z^2+z\left(x+y\right)\right]\)
\(=\left(x+y\right)\left(xy+z^2+xz+yz\right)\)
\(=\left(x+y\right)\left[\left(xy+yz\right)+\left(xz+z^2\right)\right]\)
\(=\left(x+y\right)\left[y\left(x+z\right)+z\left(x+z\right)\right]\)
\(=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Đúng 2
Bình luận (0)
a, 70a + 84b - 20ab - 24b2
= 14.(5a + 6b) - 4b(5a + 6b)
= (5a + 6b).(14 - 4b)
Đúng 0
Bình luận (0)
a, 70a + 84b - 20ab - 24b2
= (70a + 84b) - (20ab + 24b2)
= 14.(5a + 6b) - 4b.(5a + 6b)
= (5a + 6b).(14 - 4b)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử:
a. x4 + 2x3 + 10x2 - 20x
b. x3 - x2y - xy2 + y3
c. x5 + x3 - x2 - 1
phân tích các đa thức sau thành nhân tử: a) 4x(2x - 3y) - 8y(3y - 2x) b) 4x2 - 4xy + y2 - 9z2 c) x2y + yz + xy2 + xz d) (1 - x2)x2 - 16x2 - 16
Bạn thử xem lại đề câu d nhé.
Đúng 1
Bình luận (1)
a) Ta có: \(4x\left(2x-3y\right)-8y\left(3y-2x\right)\)
\(=4x\left(2x-3y\right)+8y\left(2x-3y\right)\)
\(=4\left(2x-3y\right)\left(x+2y\right)\)
b) Ta có: \(4x^2-4xy+y^2-9z^2\)
\(=\left(2x+y\right)^2-\left(3z\right)^2\)
\(=\left(2x+y+3z\right)\left(2x+y-3z\right)\)
c) Ta có: \(x^2y+yz+xy^2+xz\)
\(=xy\left(x+y\right)+z\left(x+y\right)\)
\(=\left(x+y\right)\left(xy+z\right)\)
Đúng 0
Bình luận (0)
Bài 2:Phân tích đa thức thành nhân tử chung
a, 4(2-x)2+xy-2y
b, x(x-y)3-y(y-x)2-y2(x-y)
c, x2y-xy2-3x+3y
d, x(x+y)2-y(x+y2)+xy-x2
a) \(4\left(2-x\right)^2+xy-2y\)
\(=4\left(x-2\right)^2+\left(xy-2y\right)\)
\(=4\left(x-2\right)\left(x-2\right)+y\left(x-2\right)\)
\(=\left(x-2\right)\left(4x-8\right)+y\left(x-2\right)\)
\(=\left(x-2\right)\left(4x-8+x-2\right)\)
\(=\left(x-2\right)\left(5x-10\right)\)
\(=5\left(x-2\right)^2\)
Đúng 1
Bình luận (1)
a, \(=4\left(x-2\right)^2+y\left(x-2\right)=\left(x-2\right)\left(4x-8+y\right)\)
b, \(=x\left(x-y\right)^3-y\left(x-y\right)^2-y^2\left(x-y\right)=\left(x-y\right)\left[x\left(x-y\right)^2-y\left(x-y\right)-y^2\right]=\left(x-y\right)\left[x\left(x^2-2xy+y^2\right)-xy+y^2-y^2\right]=\left(x-y\right)\left(x^3-2x^2y+xy^2-xy\right)=x\left(x-y\right)\left(x^2-2xy+y^2-y\right)\)
c, \(=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\)
d, không phân tích được
Đúng 1
Bình luận (1)
c, x2y - xy2 - 3x + 3y
= xy(x-y) - 3(x-y)
= (x-y)(x-3)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử bằng cách nhóm hạng tử
3) x2 (x+2y) - x - 2y
4) x3 - 4x2 - 9x + 36
5) x2y + xy2 + x2z + y2z + 2xyz
3) \(x^2\left(x+2y\right)-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x^2-1\right)\left(x+2y\right)\)
\(=\left(x+1\right)\left(x-1\right)\left(x+2y\right)\)
4) \(x^3-4x^2-9x+36\)
\(=\left(x^3-4x^2\right)-\left(9x-36\right)\)
\(=x^2\cdot\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x^2-9\right)\)
\(=\left(x-4\right)\left(x+3\right)\left(x-3\right)\)
Đúng 1
Bình luận (0)
\(x^2\left(x+2y\right)-x-2y\\ =x^2\left(x+2y\right)-\left(x+2y\right)\\ =\left(x^2-1\right)\left(x+2y\right)\\ =\left(x-1\right)\left(x+1\right)\left(x+2y\right)\\ ---\\ x^3-4x^2-9x+36\\ =x^2\left(x-4\right)-9\left(x-4\right)\\ =\left(x^2-9\right)\left(x-4\right)\\ =\left(x-3\right)\left(x+3\right)\left(x-4\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 2x-72x3
b) m3p+m2np-m2p2-mnp2
c) a(x2+4)-x(a2+4)
d) (xy+ab)2+(ay-bx)2
e) x2y-xy2+x3-y3
f) 4x4+1
Phân tích thành nhân tử (với a, b, x, y là các số không âm)
a ) a b + b a + a + 1 b ) x 3 - y 3 + x 2 y - x y 2
a) ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1)
= b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)
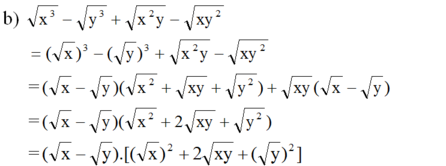
= (√x - √y)(√x + √y)2
= (√x - √y)(√x + √y)(√x + √y)
= (x - y)(√x + √y)
Đúng 0
Bình luận (0)
Phân tích thành nhân tử (với a, b, x, y là các số không âm)
x 3 - y 3 + x 2 y - x y 2
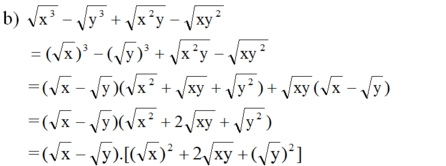
= (√x - √y)(√x + √y)2
= (√x - √y)(√x + √y)(√x + √y)
= (x - y)(√x + √y)
Đúng 0
Bình luận (0)
10 tháng 10 2021 lúc 18:08
Bài 3: Phân tích các đa thức sau thành nhân tử bằng phương pháp nhóm các hạng tửa) x4-x3-x+1 b)x2y+xy2-x-yc)ax2+a2y-7x-7y d)ax2+ay-bx2-bye)x4+x3+x+1 g)x2-2xy+y2-xz+yzh)x2-y2-x+y i)x2-4+2x+1giúp mình với,mình cần gấp mn ơi
Đọc tiếp
Bài 3: Phân tích các đa thức sau thành nhân tử bằng phương pháp nhóm các hạng tử
a) x4-x3-x+1 b)x2y+xy2-x-y
c)ax2+a2y-7x-7y d)ax2+ay-bx2-by
e)x4+x3+x+1 g)x2-2xy+y2-xz+yz
h)x2-y2-x+y i)x2-4+2x+1
giúp mình với,mình cần gấp mn ơi
a) \(=x^3\left(x-1\right)-\left(x-1\right)=\left(x-1\right)\left(x^3-1\right)\)
\(=\left(x-1\right)^2\left(x^2+x+1\right)\)
b) \(=xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\)
c) Đổi đề: \(a^2x+a^2y-7x-7y\)
\(=a^2\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(a^2-7\right)\)
d) \(=x^2\left(a-b\right)+y\left(a-b\right)=\left(a-b\right)\left(x^2+y\right)\)
e) \(=x^3\left(x+1\right)+\left(x+1\right)=\left(x+1\right)\left(x^3+1\right)\)
\(=\left(x+1\right)^2\left(x^2-x+1\right)\)
g) \(=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\)
h) \(=\left(x-y\right)\left(x+y\right)+\left(x+y\right)=\left(x+y\right)\left(x-y+1\right)\)
i) \(=\left(x+1\right)^2-4=\left(x+1-2\right)\left(x+1+2\right)=\left(x-1\right)\left(x+3\right)\)
Đúng 1
Bình luận (3)
a\(x^3\left(x-1\right)-\left(x-1\right)=\left(x-1\right)\left(x^3-1\right)\)
b)\(=xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\)
d)\(=a\left(x^2+y\right)-b\left(x^2+y\right)=\left(x^2+y\right)\left(x-b\right)\)
e)\(=x^3\left(x+1\right)+\left(x+1\right)=\left(x+1\right)\left(x^3+1\right)\)
g)\(=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\)
h)\(=\left(x-y\right)\left(x+y\right)-\left(x-y\right)=\left(x-y\right)\left(x+y-1\right)\)
i)\(=\left(x-1\right)^2-4=\left(x-1-2\right)\left(x-1+2\right)=\left(x-3\right)\left(x+1\right)\)
Đúng 9
Bình luận (5)