tìm nghiệm nguyên của phương trình x2-xy-3x+4y+1=0

Những câu hỏi liên quan
Tìm nghiệm nguyên x,y của phương trình biết:
3x .x2 -4y2 -4y=0
Lời giải:
$3^x.x^2=4y(y+1)$ nên $x$ chẵn. Đặt $x=2a$ ta có:
$3^{2a}.a^2=y(y+1)\Leftrightarrow (3^a.a)^2=y(y+1)$
Dễ thấy $(y,y+1)=1$ nên để tích của chúng là scp thì $y,y+1$ là scp.
Đặt $y=m^2; y+1=n^2$ với $m,n$ tự nhiên.
$\Rightarrow 1=(n-m)(n+m)$
$\Rightarrow n=1; m=0\Rightarrow y=0\Rightarrow x=0$
Đúng 0
Bình luận (0)
Tập nghiệm của pt: x4-8x ²-90Hệ pt: x2+y2+xy7 x2+y2-xy3có nghiệm là.Cho phương trình(x2-3x+3)2-2x2+6x-50 Nếu đặt tx2-3x+3thì phương trình đã cho trở thành phương trình nào Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằngA. -3.B. 2.C. 18.D. 21.
Đọc tiếp
Tập nghiệm của pt: x4-8x ²-9=0
Hệ pt: x2+y2+xy=7
x2+y2-xy=3
có nghiệm là.
Cho phương trình(x2-3x+3)2-2x2+6x-5=0 Nếu đặt t=x2-3x+3
thì phương trình đã cho trở thành phương trình nào
Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2
có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằng
A. -3.
B. 2.
C. 18.
D. 21.
Tìm nghiệm nguyên phương trình
\(x^2-xy-3x+4y+1=0\)
=>(x-4) y =x2 -3x +1
+ nếu x =4 => x2 -3x +1 không có nghiệm nghuyên.
+ Nếu x khác 4 => \(y=\frac{x^2-3x+1}{x-4}=x+1+\frac{5}{x-4}\)
x ;y thuộc z => x-4 thuộc U(5) ={-5;-1;1;5}
| x-4 | -5 | -1 | 1 | 5 |
| x | -1 | 3 | 5 | 9 |
| y | -1 | -1 | 11 | 11 |
Đúng 0
Bình luận (0)
tìm phương trình nghiệm nguyên: x2 - 3x + 9 = -xy +2y
Lời giải:
$x^2-3x+9=-xy+2y$
$\Leftrightarrow x^2+x(y-3)+(9-2y)=0$
Coi đây là pt bậc 2 ẩn $x$. PT có nghiệm nguyên khi:
$\Delta=(y-3)^2-4(9-2y)=m^2$ với $m$ là stn.
$\Leftrightarrow y^2+2y-27=m^2$
$\Leftrightarrow (y+1)^2-28=m^2$
$\Leftrightarrow 28=(y+1)^2-m^2=(y+1-m)(y+1+m)$
Do $y+1-m, y+1+m$ là các số nguyên và có cùng tính chẵn lẻ, $y+1-m\leq y+1+m$ với $m$ tự nhiên nên:
TH1: $y+1-m=2; y+1+m=14$
$\Rightarrow y=7$. Thay vào pt và giải tìm x thôi.
TH2: $y+1-m=-14; y+1+m=-2$
$\Rightarrow y=-9$. Đến đây thay vào pt ban đầu và giải tìm $x$.
Đúng 1
Bình luận (0)
Tìm nghiệm nguyên của phương trình sau:
(x2 - x +1)(y2 + xy) = 3x - 1
bài này dễ quá 😖 mấy a/c giúp e với
tìm nghiệm nguyên của phương trình 3x^2+4y^2+6x+3y-4=0
Tìm nghiệm nguyên của phương trình sau
a,x^2 -xy =6x-5y-8
b, 3x^2 -4y^2=13
a)
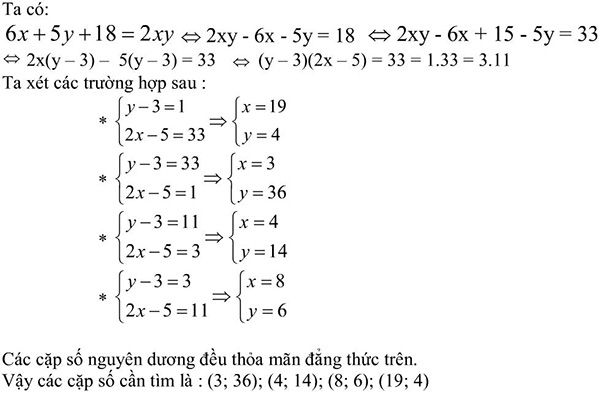
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình 3x^2+4y^2+4x+3y-4=0
Tìm nghiệm nguyên của phương trình 3x^2+4y^2+4x+3y-4=0
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) x2 + y2 + xy + 4x – 2 = 0;
b) x2 + y2 – 2x – 4y + 5 = 0;
c) x2 + y2 + 6x – 8y + 1 = 0.
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
Đúng 0
Bình luận (0)














