\(5\left(3x^{n+1}-y^{n-1}\right)-3\left(x^{n+1}+2y^{n-1}\right)+4\left(-x^{n+1}+2y^{n-1}\right)\)

\(=15x^{n+1}-5y^{n-1}-3x^{n+1}-6y^{n-1}-4x^{n+1}+8y^{n-1}\)

\(=8x^{n+1}-3y^{n-1}\)

a: \(x^{n}\cdot y^{n+2}\left(xy+x^2y+1\right)\)

\(=x^{n}\cdot y^{n+2}\cdot xy+x^{n}\cdot y^{n+2}\cdot x^2y+x^{n}y^{n+2}\)

\(=x^{n+1}\cdot y^{n+3}+x^{n+2}\cdot y^{n+3}+x^{n}y^{n+2}\)

b: \(\left(4x^{n-2}+x^{n+1}\right)\cdot x^{n}\)

\(=4x^{n-2}\cdot x^{n}+x^{n+1}\cdot x^{n}\)

\(=4x^{2n-2}+x^{2n+1}\)

c: \(4xy\left(x^{n-2}y^{n+1}+x^{n}y^{n+1}\right)\)

\(=4xy\cdot x^{n-2}\cdot y^{n+1}+4xy\cdot x^{n}y^{n+1}\)

\(=4x^{n-1}y^{n+2}+4x^{n+1}\cdot y^{n+2}\)

\(4xy\left(x^{n-2}y^{n+1}+x^{n}y^{n+1}\right)\)

\(=4xy\cdot x^{n-2}\cdot y^{n+1}+4xy\cdot x^{n}y^{n+1}\)

\(=4x^{n-1}y^{n+2}+4x^{n+1}\cdot y^{n+2}\)

4x\(^{1+n-2}\)y\(^{1+n+1}\)4xy\(^{1+n}\)+4xy

Sửa đề: \(4xy\left(x^{n-2}y^{n+1}+x^{n}\cdot y^{n+1}\right)\)

\(4xy\left(x^{n-2}y^{n+1}+x^{n}y^{n+1}\right)\)

\(=4xy\cdot x^{n-2}\cdot y^{n+1}+4xy\cdot x^{n}y^{n+1}\)

\(=4x^{n-1}y^{n+2}+4x^{n+1}\cdot y^{n+2}\)

Chọn A.

Ta có: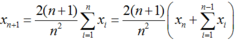 

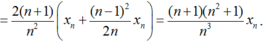
Do đó: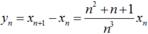 

- Ta chứng minh dãy (y_n)  tăng.

Ta có: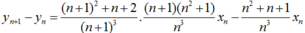 

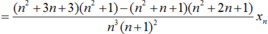
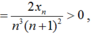
- Ta chứng minh dãy (y_n)  bị chặn.

Trước hết ta chứng minh: x_n ≤ 4(n – 1) (1)

 * Với n = 2, ta có: x₂ = 4x₁ = 4 nên (1) đúng với n = 2

 * Giả sử (1) đúng với n, tức là: x_n ≤ 4(n – 1), ta có

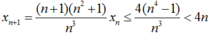
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng

Ta có: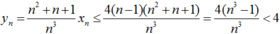 

Vậy bài toán được chứng minh.

`@` `\text {Ans}`

`\downarrow`

\(x^n\cdot y^{n+2}\cdot\left(xy+x^2y+1\right)\)

`=`\(x^n\cdot y^n\cdot y^2\left(xy+x^2y+1\right)\)

`=`\(\left(xy\right)^n\cdot y^2\cdot xy+y^2\cdot x^2y+y^2\)

`=`\(\left(xy\right)^n\cdot xy^3+x^2y^3+y^2\)