Cho △ABC (∠A=900); BD là tia p/giác của B (D∈GAC). Trên tia BC lấy điểm E sao cho BA=BE
a) Chứng minh △BAD=△BED=>DE⊥BE
b) Chứng minh BD là đường trung trực của AE
c) Kẻ AH⊥BC. So sánh EH và EC
Cho tam giác ABC ( ∠ A = 90 0 ) có đường cao AH. Chứng minh rằng A H 2 = B H . C H
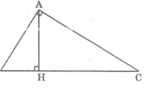
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: 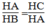
Vậy A H 2 = B H . C H
Cho Δ ABC và Δ MNP có A ^ = M ^ = 90 0 , AB/MN = BC/NP thì?
A. Δ ABC ∼ Δ PMN
B. Δ ABC ∼ Δ NMP
C. Δ ABC ∼ Δ MNP
D. Δ ABC ∼ Δ MPN
Ta có: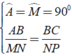
⇒ Δ ABC ∼ Δ MNP ( c - g - c )
Chọn đáp án C.
Cho tam giác ABC vuông tại A; BC = a không đổi, C ^ = α 0 0 < α < 90 0
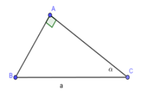
Lập công thức để tính diện tích tam giác ABC theo a và
A. 1 2 a 2 sin α . cos α
B. a 2 sin α . cos α
C. 2 a 2 sin α . cos α
D. 3 a 2 sin α . cos α
Xét ∆ ABC vuông tại A ta có: A B = B C . sin α = a . sin α A C = B C . cos α = a . c o s α
![]()
Đáp án cần chọn là: A
cho tam giác abc có góc A =900 trung tuyển AM=5cm thì cạch huyền BC bằng
Cho tam giác ABC có ![]() , biết
, biết ![]() . Số đo của góc A là:
. Số đo của góc A là:
A. 300 B. 600 C.900 D. 1200
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD. Chứng minh rằng ∠(EAF) = 900.
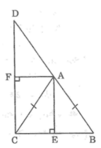
Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
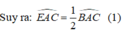
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
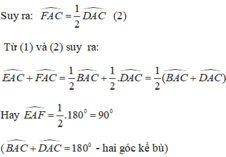
Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với đáy (ABC); SA = AB = a, AC = 2a và A S C ^ = A B C ^ = 90 0 . Tính theo a thể tích khối chóp S.ABC.
A . a 3 2 4
B . 3 a 3 4
C . a 3 4
D . a 3 3 4
Đáp án C.
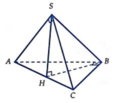
Kẻ SH ⊥ AC, do (SAC) ⊥ (ABC)=> SH ⊥ (ABC)
Có BC = ![]()
![]()
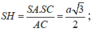

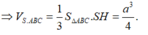
Cho tam giác ABC A= 900 . Qua trung điểm I của AC, dựng ID ⊥ BC. Chứng minh : BD2-CD2=AB2
Cho tam giác ABC vuông cân tại A, số đo góc B bằng
A. 600 | B. 900 | C. 450 | D. 1200 |
\(\widehat{A}=90^o\) \(\Rightarrow\widehat{B}+\widehat{C}=180^o-90^o=90^o\)
Do tam giác ABC la tam giac cân \(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{90^o}{2}=45^o\)
Chọn C
C
+)Do ΔABC là tam giác vuông cân tại A
=>\(\widehat{A}=90^o,\widehat{B}=\widehat{C}\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=90^o\)
\(=>\widehat{B}+\widehat{C}=180^o-\widehat{A}\)
\(=>\widehat{B}+\widehat{C}=180^o-90^o=90^o\)
Mà \(\widehat{B}=\widehat{C}=>\widehat{B}=\dfrac{90^o}{2}=45^o\)
Cho tam giác ABC vuông tại A; BC = a không đổi, C ^ = α 0 0 < α < 90 0
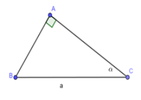
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.
A. α = 45 0 ; m a x S A B C = 1 2 a 2 .
B. α = 30 0 ; m a x S A B C = 3 4 a 2 .
C. α = 60 0 ; m a x S A B C = 3 4 a 2 .
D. α = 45 0 ; m a x S A B C = 1 4 a 2 .
S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
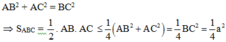
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
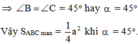
Đáp án cần chọn là: D