Tính sinα biết rằng α=π/3 +kπ,k € Z
Giúp em với
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
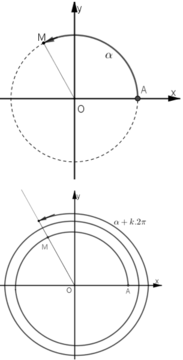
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
Biết sinα = 3/4 và π/2 < α < π. Tính
![]()
Tính cos(α-π/3) biết sinα=3/5 và π/2
Lời giải:
$\cos^2 a=1-\sin^2a=1-(\frac{3}{5})^2=\frac{16}{25}$
$\Rightarrow \cos a=\pm \frac{4}{5}$
Ta có:
\(\cos (a-\frac{\pi}{3})=\cos a\cos \frac{\pi}{3}-\sin a\sin \frac{\pi}{3}\)
\(=\frac{1}{2}\cos a-\frac{3\sqrt{3}}{10}=\frac{1}{2}.\pm \frac{4}{5}-\frac{3\sqrt{3}}{10}\)
Biểu diễn trên đường tròn lượng giác góc (cung) có số đo α:
a) α = 10350
b) α = 195π/3
c) α = π/2 + kπ, k∈Z
d) α = kπ
Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2
Chứng minh rằng với mọi α, ta luôn có
cos(α + π/2) = -sinα
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Đặt u = π/2 - x thì u' = -1
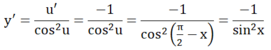
Do cos(π/2-x) = sinx
Cho góc α thỏa mãn: π 2 < α < π và sin α + π .Tính tan 7 π 3 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc α thỏa mãn π 2 < α < π và sin α + π = - 1 3 Tính tan 7 π 2 - α .
A. 3 2
B. - 2
C. - 2 2
D. 4 2