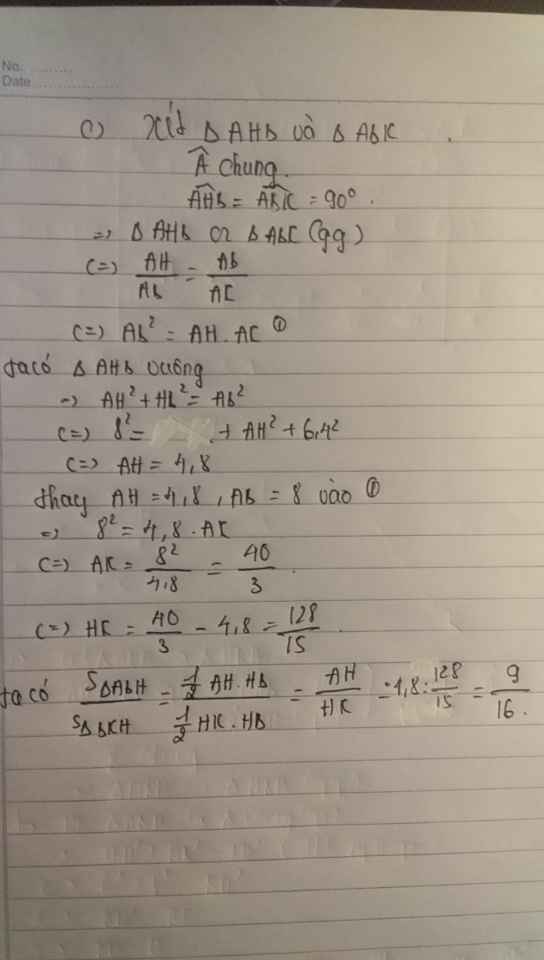Cho hình chữ nhật ABCD có AB =6 , AC = 10. Vẽ đường cao AH của tam giác ABD. Tính CH

Những câu hỏi liên quan
cho hình chữ nhật ABCD có AB=8cm; BC=6cm. vẽ đường cao AH của tam giác ABD hãy chứng minh tam giác AHD đồng dạng với tam giác BAD
Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Vẽ đường cao AH của tam giác ABD.
a) CM : Tam giác AHB đồng dạng với tam giác BCD
b) \(AD^2=DH.DB\)
c) Tính DH, AH.
a) vì ABCD là hình chữ nhật
nên AB // DC => góc ABH= góc BDC ( 2 góc so le trong )
Xét 2 tam giác AHB và BCD có
góc ABH = góc BDC
góc AHB = góc BCD =900
=> 2 tam giác AHB và BCD đồng dạng (g.g)
b) Xét 2 tam giác ADH và BDA có
góc ADH chung
góc AHD = góc BAD =900
nên 2 tam giác ADH và BDA là 2 tam giác đồng dạng (g.g)
=> \(\frac{AD}{BD}=\frac{DH}{AD}\)
=> AD2=BD.DH
tam giác ABD vuông tại A
=> \(BD^2=AD^2+AB^2\)( Py-ta-go)
=>BD =10cm
mà AD2=DH.BD (cmt)
=> 62=DH.10
=> DH =3.6cm
tam giác ADH vuông tại H nên AD2=AH2+DH2 ( py-ta-go)
<=> 62-3.62=AH2
AH=\(\sqrt{6^2-3.6^2}\)=4.8cm
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 8cm; BC = 6cm. Vẽ đường cao AH của tam giác ABD. Hãy
a) Chứng minh Tam giác AHB Đồng dạnh Tam giác BCD
b) Chứng minh : Tam giác AHD Đồng dạng Tam giác BAD
c) Tính diện tích tam giác ABD, từ đó tính độ dài đoạn thẳng AH ?
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
Do đó: ΔAHD\(\sim\)ΔBAD
Đúng 1
Bình luận (0)
Bài 2: Cho tam giác ABC vuông ở A, có AB 6cm; AC 8cm. Vẽ đường cao AH.a) Tính BC. b) Chứng minh AB2 BH.BC c) Tính BH; HC.Bài 3: Cho hình chữ nhật ABCD có AB 8cm, BC 6cm. Vẽ đường cao AH của tam giác ADB, (H BD) a) Chứng minh DAHB DBCD. b) Chứng minh AD2 HD.DB.c) Tính độ dài đoạn thẳng DH. cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
Đọc tiếp
Bài 2: Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a) Tính BC.
b) Chứng minh AB2 = BH.BC
c) Tính BH; HC.
Bài 3: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB, (H![]() BD)
BD)
a) Chứng minh DAHB ![]() DBCD.
DBCD.
b) Chứng minh AD2 = HD.DB.
c) Tính độ dài đoạn thẳng DH.
cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
thui hong cần nữa, hong cíu thì thui tui tự làm liu liu 
Đúng 1
Bình luận (5)
cho hình chữ nhật ABCD có AB = 8cm, BC = 6 cm. vẽ đường cao AH của tam giác ABD
a. cm tam giác AHB = tam giác BCD
b. cm AD^2 = DH.DB
c. tính đọ dài đoạn thẳng DH và AH
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{BAH}=\widehat{DBC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: Xét ΔADB vuông tại A có AH là đường cao
nên \(AD^2=DH\cdot DB\)
c: BD=10(cm)
=>DH=3,6cm
=>BH=6,4(cm)
=>AH=4,8cm
Đúng 2
Bình luận (0)
sửa đề là đồng dạng bạn nhé
a, Xét tam giác AHB và tam giác BCD có :
^AHB = ^BCD = 900 ; ^ABH = ^BDC ( soletrong )
Vậy tam giác AHB ~ tam giác BCD ( g.g )
b, Xét tam giác ADH và tam giác DBC có :
^ADH = ^DBC ( soletrong) ; ^AHD = ^BCD = 900
Vậy tam giác ADH ~ tam giác DBC (g.g)
\(\dfrac{DH}{BC}=\dfrac{AD}{DB}\Rightarrow AD.BC=DH.DB=AD^2\)
c, Theo định lí Pytago tam giác ABD vuông tại A
\(BD=\sqrt{AD^2+AB^2}=10cm\)
Ta có : \(DH=\dfrac{AD^2}{DB}=\dfrac{18}{5}cm\)
Lại có : tam giác AHB ~ tam giác BCD ( g.g ) (cmt)
\(\dfrac{AH}{BC}=\dfrac{AB}{BD}\Rightarrow AH=\dfrac{AB.BC}{BD}=\dfrac{24}{5}cm\)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB 4cm, BC 3cm. Vẽ đường cao AH của tam giác ADB ( H thuộc BD).a/ Chứng minh ∆ABD đồng dạng với ∆ HBAb/ Tính độ dài BD, HB.c/ Kẻ đường phân giác AE của góc BAD ( E thuộc BD). Chứng minh:
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 4cm, BC = 3cm. Vẽ đường cao AH của tam giác ADB ( H thuộc BD).
a/ Chứng minh ∆ABD đồng dạng với ∆ HBA
b/ Tính độ dài BD, HB.
c/ Kẻ đường phân giác AE của góc BAD ( E thuộc BD). Chứng minh:
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc ABD chung
=>ΔABD đồng dạng với ΔHBA
b: BD=căn 3^2+4^2=5cm
HB=AB^2/BD=3,2cm
c: AD là phân giác
=>ED/EB=AD/AB
mà AD/AB=AH/BH
nên ED/EB=AH/BH
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Vẽ đường cao AH của tam giác ADB a) Chứng minh AD bình = DH.DB b) Tính DH
a: Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
góc HDA chung
=>ΔDHA đồng dạng với ΔDAB
=>DH/DA=DA/DB
=>DA^2=DH*DB
b: DB=căn 8^2+6^2=10cm
DH=6^2/10=3,6cm
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 8cm, AD = 6cm. Kẻ đường cao AH của tam giác ABD.
a) Chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b) Tính độ dài các đoạn thẳng BD, HB.
c) Đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. Tính tỉ số diện tích của hai tam giác ABH và BKH.
Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của tam giác ADB.
a) Chứng minh Tam giác AHB đồng dạng với tam giác BCD.
b) Tính độ dài đoạn thẳng AH .
c) Tính diện tích tam giác AHB