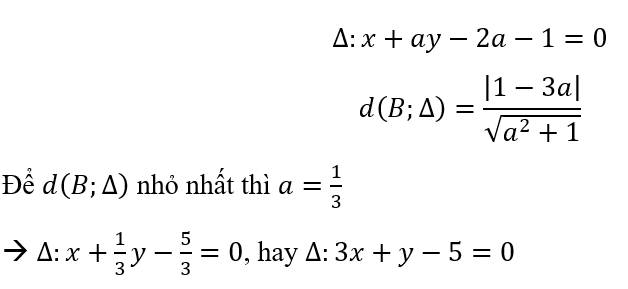Cho điểm M(3:5) và đường thẳng đenta có phương trình x-3y-6=0. Tính khoảng cách từ M đến đenta

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;2), B(2;-1). Đường thẳng đenta đi qua điểm A, sao cho khoảng cách từ điểm B đến đường thẳng đenta nhỏ nhất có phương trình là?
trên mặt phẳng tọa độ oxy, cho 3 điểm A(1,1), B(3,2), C(7,10)lập phương trình đường thẳng đenta đi qua A sao cho tổng khoảng cách từ B,C đến đường thẳng đenta là lớn nhất.
xác định đường thẳng d : y =ax+b đi qua điểm M(1;2) và song song đường thẳng đenta : y=x+6 tinhs khoảng cách từ 0 đến đường thẳng d
cho điểm A (4;-7) và đường thẳng đenta x-2y+4=0 .tìm điểm b trên đenta sao cho đúng 3 đường thẳng d1,d2,d3 thỏa mãn khoảng cách từ A đến d1,d2,d3 đều bằng 4 và khoảng cách từ B đến d1,d2,d3 bằng 6
help me![]()
cho 2 điểm A( 1;-2), C(3;0)
- Viết phương trình đường thằng Đenta đi qua A và cách C một khoảng bằng 3
\(AC=\sqrt{\left(3-1\right)^2+\left(0+2\right)^2}=2\sqrt{2}< 3\)
\(\Rightarrow\) Không tồn tại đường thẳng denta thỏa mãn yêu cầu đề bài
Đúng 0
Bình luận (0)
xác định đường thẳng d : y = ax+b đi qua điểm M(1;2) và song song đường thẳng đenta : y = x+6 tính khoang cách từ 0 đến đường thẳng d
Vì (d)//(Δ) nên a=1
Vậy: y=x+b
Thay x=1 và y=2 vào (d), ta được:
b+1=2
hay b=1
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, tìm điểm M(a;b) (a>0) thuộc đường thẳng d: x=3+t; y=2+t và cách đường thẳng đenta: 2x-y-3=0 một khoảng 2√5
M thuộc d nên tọa độ có dạng:
\(M\left(t+3;t+2\right)\) với \(t>-3\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2\left(t+3\right)-\left(t+2\right)-3\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)
\(\Leftrightarrow\left|t+1\right|=10\Rightarrow\left[{}\begin{matrix}t=9\\t=-11\left(l\right)\end{matrix}\right.\)
\(\Rightarrow M\left(12;11\right)\)
Đúng 0
Bình luận (0)
Cho đường thẳng đenta: x+y-3=0
a) A(1;-1) B(0;1) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
b) A(1;-1) B(2;3) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
Làm bừa coi xem đk :b
\(M\in\Delta:y=3-x\Rightarrow M\left(x;3-x\right)\)
a/ MA+MB min
\(MA=\sqrt{\left(x_A-x_M\right)^2+\left(y_A-y_M\right)^2};MB=\sqrt{\left(x_B-x_M\right)^2+\left(y_B-y_M\right)^2}\)
\(Minkovsky:MA+MB\ge\sqrt{\left(x_M-x_A+x_M-x_B\right)^2+\left(y_M-y_A+y_M-y_B\right)^2}\)
\("="\Leftrightarrow\dfrac{x_A-x_M}{y_A-y_M}=\dfrac{x_B-x_M}{y_B-y_M}\Leftrightarrow\dfrac{1-x}{-1-3+x}=\dfrac{-x}{1-3+x}\)
\(\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
|MA-MB| max
\(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{1+4}=\sqrt{5}\)
Theo bdt tam giác ta luôn có: \(\left|MA-MB\right|\le AB\)
\(\Leftrightarrow\left|\sqrt{\left(x_M-1\right)^2+\left(y_M+1\right)^2}-\sqrt{x_M^2+\left(y_M-1\right)^2}\right|\le\sqrt{5}\)
\("="\Leftrightarrow M,A,B-thang-hang\)
\(\Leftrightarrow\overrightarrow{MA}=k\overrightarrow{MB}\Leftrightarrow\left\{{}\begin{matrix}x_A-x_M=k\left(x_B-x_M\right)\\y_A-y_M=k\left(y_B-y_M\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1-x}{-x}=\dfrac{-4+x}{-2+x}\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
Câu b tương tự bạn tự làm nốt
Đúng 0
Bình luận (0)
Cho điểm A(1,2,3)
đenta 1\(\left\{{}\begin{matrix}x=2-t\\y=t\\z=-1+2t\end{matrix}\right.\)
đenta 2 \(\left\{\dfrac{x+1}{1}=\dfrac{y}{1}=\dfrac{z-2}{-1}\right\}\)
a) Lập phương trình đường thẳng đenta1, đenta2 và vuông góc với mặt phẳng (P): x+y+z=0
b) Lập phương tình đường vuông góc chung của đường thẳng đenta 1 , đenta2