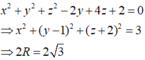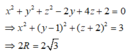Tìm nghiệm nguyên tố của phương trình: x2 + y2 + z2 = xyz

Những câu hỏi liên quan
1. tìm nghiệm nguyên của phương trình:
p(x + y) = xy và p nguyên tố
2. tìm nghiệm nguyên của phương trình:
a. x + y + z + 9 = xyz
b. x + y + 1 = xyz
Tìm tất cả các nghiệm nguyên dương của phương trình: x2=xyz+2z+2
Tìm nghiệm nguyên của phương trình: x4+x2+1=y2
Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình : x2 - xy +y2 = x-y
<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
Đúng 0
Bình luận (0)
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0
Đúng 0
Bình luận (0)
Tìm các nghiệm nguyên của phương trình sau: 7(x2+y2) = 25(x+y)
Tìm giải phương trình nghiệm nguyên : x2 = y2
Bài 1: Tìm các số x; y; z biết rằng:
a) và xyz = 810; b) và x2 + y2 + z2 = 14.
b) và x2 + y2 + z2 = 14.
Tập nghiệm của pt: x4-8x ²-90Hệ pt: x2+y2+xy7 x2+y2-xy3có nghiệm là.Cho phương trình(x2-3x+3)2-2x2+6x-50 Nếu đặt tx2-3x+3thì phương trình đã cho trở thành phương trình nào Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằngA. -3.B. 2.C. 18.D. 21.
Đọc tiếp
Tập nghiệm của pt: x4-8x ²-9=0
Hệ pt: x2+y2+xy=7
x2+y2-xy=3
có nghiệm là.
Cho phương trình(x2-3x+3)2-2x2+6x-5=0 Nếu đặt t=x2-3x+3
thì phương trình đã cho trở thành phương trình nào
Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2
có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằng
A. -3.
B. 2.
C. 18.
D. 21.
Tìm độ dài đường kính của mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
−
2
y
+
4
z
+
2
0.
A.
2
3
B. 2. C. 1. D.
3
Đọc tiếp
Tìm độ dài đường kính của mặt cầu (S) có phương trình x 2 + y 2 + z 2 − 2 y + 4 z + 2 = 0.
A. 2 3
B. 2.
C. 1.
D. 3
Tìm độ dài đường kính của mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-2y+4z+2 0
Đọc tiếp
Tìm độ dài đường kính của mặt cầu (S) có
phương trình x 2 + y 2 + z 2 -2y+4z+2 = 0
![]()
![]()
![]()
![]()