Cho tứ giác lồi ABCD có diện tích S. CMR: 2S \(\le\) BD. (AD + BC)

Những câu hỏi liên quan
Cho tứ giác lồi ABCD có diện tích S và O là điểm nằm trong tứ giác sao cho OA^2+OB^2+OC^2+OD^2=2S. Chứng minh rằng ABCD là hình vuông có tâm là O
Cho tứ giác lồi ABCD. Gọi M, N theo thứ tự là trung điểm của AD, BC.
a) nếu biết diện tích ABM bằng 3cm và diện tích tam giác CDN bằng 4cm tính diện tích tứ giác ABCD
Cho tứ giác lồi ABCD có đường chéo AC bằng cạnh AD. C/minh: BC < BD
Cho tứ giác lồi ABCD có đường chéo AC bằng cạnh AD. C/minh: BC < BD
Cho tứ giác lồi ABCD có các đường chéo \(AC = x,BD = y\) và góc giữa AC và BD bằng \(\alpha .\) Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh \(S = \frac{1}{2}xy.\sin \alpha \)
b) Nêu kết quả trong trường hợp \(AC \bot BD.\)
Tham khảo:

Gọi O là giao điểm của AC và BD.
a) Áp dụng công thức \(S = \frac{1}{2}ac.\sin B\), ta có:
\(\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}.OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}\)
Mà \(\sin ({180^o} - \alpha ) = \sin \alpha \)
\( \Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .\)
\(\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha = \frac{1}{2}.x.y.\sin \alpha .\end{array}\)
b) Nếu \(AC \bot BD\) thì \(\alpha = {90^o} \Rightarrow \sin \alpha = 1.\)
\( \Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.\)
Đúng 0
Bình luận (0)
tứ giác lồi ABCD có AD = BC, AC = BD. Chứng minh ABCD là hình thang cân
Xét tứ giác ABCD
Ta có:AD=BC và AC=BD(gt)
-> tứ giác ABCD là hính thang cân (t/c hình thang cân)
Đúng 0
Bình luận (0)
bạn tự vẽ hình nhé
Xét tứ giác ABCD
Ta có:AD=BC và AC=BD(gt)
-> tứ giác ABCD là hính thang cân (t/c hình thang cân)
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD. Gọi M,N,P,Q,E,F lần lượt là trung điểm của AB , CD, AD, BD, AC. BC CMR: MN, PQ, EF đồng quy.
Ta có : Tứ giác MPNQ là hình bình hành
MN và PQ cắt nhau tại trung điểm I của mỗi đường
Ta có : Tứ giác EPFQ là hình bình hành
EF đi qua I
Vậy EF , MN và PQ đồng quy
Cho tứ diện ABCD có ABACAD2a. Biết tam giác BCD có BC2a, BDa,
C
B
D
^
120
°
. Tính thể tích tứ diện ABCD theo a
Đọc tiếp
Cho tứ diện ABCD có AB=AC=AD=2a. Biết tam giác BCD có BC=2a, BD=a, C B D ^ = 120 ° . Tính thể tích tứ diện ABCD theo a
![]()
![]()
![]()
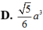
Cho tứ diện ABCD có AB AC AD 2a. Biết tam giác BCD có BC 2a, BD a,
C
B
D
^
120
0
. Tính thể tích tứ diện ABCD theo a. A.
5
3
a
3
B.
5
2
a
3...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, C B D ^ = 120 0 . Tính thể tích tứ diện ABCD theo a.
A. 5 3 a 3
B. 5 2 a 3
C. 5 a 3
D. 5 6 a 3
Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
Cách giải:
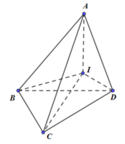
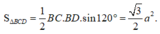
![]()
![]()
Ta có: ![]()
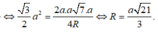
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 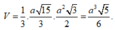
Chọn D.
Đúng 0
Bình luận (0)