Cho sin(40o+a)=a (0o<a<45o). Tính cos(70o+a)

Những câu hỏi liên quan
với 0o < a < 90o cho sin a = 3 cos a khi đó tính 4 - sina cosa tâ được kết quả là:
A.3
B.3,5
C.3,7
D.3,9
\(\sin^2\alpha+\cos^2\alpha=1\Leftrightarrow10\cos^2\alpha=1\Leftrightarrow\cos\alpha=\sqrt{\dfrac{1}{10}}=\dfrac{\sqrt{10}}{10}\\ \Leftrightarrow\sin\alpha=\dfrac{3\sqrt{10}}{10}\\ \Leftrightarrow4-\sin\alpha\cdot\cos\alpha=4-\dfrac{\sqrt{10}\cdot3\sqrt{10}}{100}=4-\dfrac{3}{10}=3,7\)
Vậy chọn C
Đúng 1
Bình luận (0)
Chiếu một tia sáng lên một bề mặt phẳng phản xạ ánh sáng , ta thu được một tia phản xạ tạo với tia tới một góc 00 . Tìm giá trị góc tới .
A.
0o.
B.
80o
C.
40o
D.
60o
Xem thêm câu trả lời
Góc hợp bởi tia tới với mặt một gương phẳng đo được là 40o thì góc phản xạ:
A. 60o B. 90o C. 0o D. 50o
\(i=90^o-40^o=50^o\)
\(i=i'\Leftrightarrow i'=50^o\)
\(\Rightarrow D\)
Đúng 5
Bình luận (2)
Xem thêm câu trả lời
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) tan2x = \(\dfrac{sin^{2_{ }}x}{cos^{2_{ }}x}\) ( x≠90o)
b) cot2x = \(\dfrac{cos^2x}{sin^2x}\) ( x ≠ 0o)
a: Ta sẽ có hình vẽ sau:
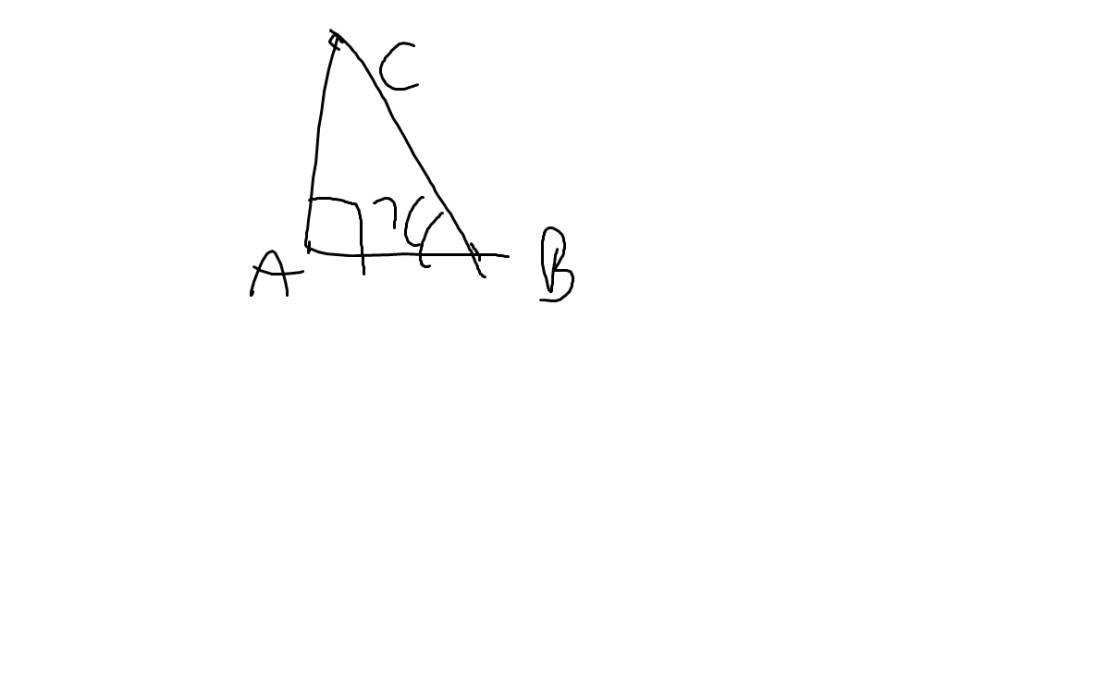
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
Đúng 2
Bình luận (0)
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) sin x = \(\sqrt{1-cos^{2_{ }}x}\)
b) cos x = \(\sqrt{1-sin^{2_{ }}x}\)
a: \(sin^2x+cos^2x=1\)
=>\(sin^2x=1-cos^2x\)
=>\(sinx=\sqrt{1-cos^2x}\)
b: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x\)
=>\(cosx=\sqrt{1-sin^2x}\)
Đúng 2
Bình luận (0)
Cho 0o < x < 90o, CM các biểu thức sau không phụ thuộc vào biến:
\(\dfrac{\tan^2x-\cos^2x}{\sin^2x}+\dfrac{\cot^2x-\sin^2x}{\cos^2x}\)
ta có : \(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}=\dfrac{1}{cos^2x}-cot^2x+\dfrac{1}{sin^2x}-tan^2x\)
\(=\dfrac{1}{cos^2x}-tan^2x+\dfrac{1}{sin^2x}-cot^2x=\dfrac{1}{cos^2x}-\dfrac{sin^2x}{cos^2x}+\dfrac{1}{sin^2x}-\dfrac{cos^2x}{sin^2x}\)
\(=\dfrac{1-sin^2x}{cos^2x}+\dfrac{1-cos^2x}{sin^2x}=\dfrac{cos^2x}{cos^2x}+\dfrac{sin^2x}{sin^2x}=1+1=2\) không phụ thuộc vào \(x\) (đpcm)
Đúng 0
Bình luận (0)
Cho ΔABC = ΔDIK. ∠B = 50o, ∠K = 40o. Điền vào chỗ trống: ∠ A = ……
Ta có: ΔABC = ΔDIK nên ∠A = ∠D; ∠B= ∠I ; ∠C = ∠K
Suy ra: ∠I = 50°; ∠C = 40°
Xét tam giác ABC ta có:
∠A + ∠B +∠C = 180° nên:
∠A = 180° –( ∠B+∠C) = 180° –(50° +40°) = 90°
Do đó: ∠A = 90°
Đúng 0
Bình luận (0)
Cho hình vẽ sau: Biết
a
∥
b
,
A
1
^
-
C
1
^
40
o
. Tính
A
2
^
,
C
2
^
A.
A...
Đọc tiếp
Cho hình vẽ sau:
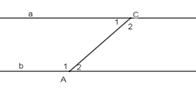
Biết a ∥ b , A 1 ^ - C 1 ^ = 40 o . Tính A 2 ^ , C 2 ^
A. A 2 ^ = 80 ° , C 2 ^ = 110 °
B. A 2 ^ = 110 ° , C 2 ^ = 70 °
C. A 2 ^ = 70 ° , C 2 ^ = 110 °
D. A 2 ^ = 70 ° , C 2 ^ = 70 °
Cho hình vẽ sau Biết
a
⊥
y
,
b
⊥
y
,
A
1
^
-
B
1
^
40
o
. Tính
B
1
^
A. 110
°
B. 70
°
C. 80
°
D. 90...
Đọc tiếp
Cho hình vẽ sau
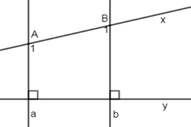
Biết a ⊥ y , b ⊥ y , A 1 ^ - B 1 ^ = 40 o . Tính B 1 ^
A. 110 °
B. 70 °
C. 80 °
D. 90 °
Tam giác ABC có ∠A = 40o. Các tia phân giác của các góc B và C cắt nhau ở I.
Góc BIC bằng:
(A) 40o;
(B) 70o;
(C) 110o;
(D) 140o.
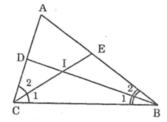
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C
Đúng 0
Bình luận (0)
























