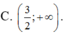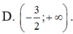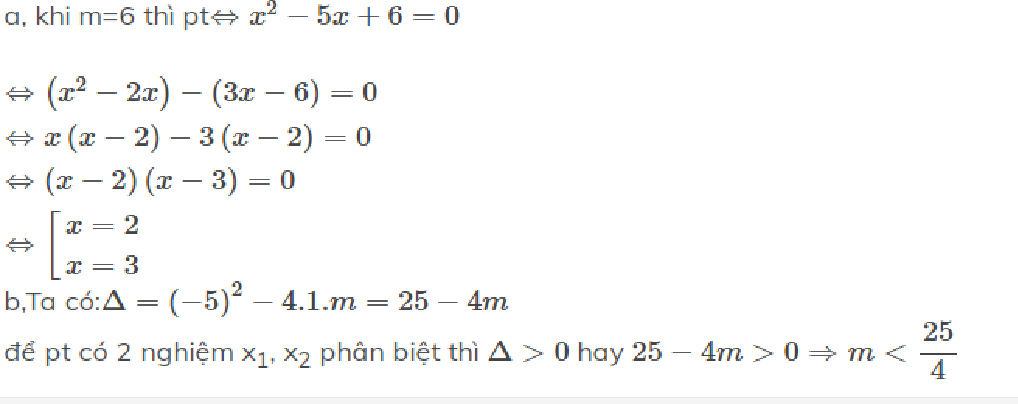cho phương trình \(3x^2+5x-6=0\) có 2 nghiệm phân biệt: x1;x2.Ko giải pt hãy lập pt bậc hai có các nghiệm : y1= x1+\(\frac{1}{x_2}\)và y2=x2+\(\frac{1}{x_1}\)

Những câu hỏi liên quan
tìm m để phương trình: 3x^2 - 5x + m = 0 có 2 nghiệm phân biệt x1, x2 sao cho 6x1 + x2 = 0
Theo hệ thức Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\left(1\right)\\x_1x_2=\dfrac{m}{3}\left(2\right)\end{matrix}\right.\)
Ta có \(6x_1+x_2=0\)\(\Rightarrow5x_1+\left(x_1+x_2\right)=0\Rightarrow5x_1+\dfrac{5}{3}=0\Leftrightarrow x_1=-\dfrac{1}{3}\) Thay vào (1) ta được:
\(x_2-\dfrac{1}{3}=\dfrac{5}{3}\Rightarrow x_2=2\)
Thay \(x_1=-\dfrac{1}{3};x_2=2\) vào (2) ta được:
\(-\dfrac{2}{3}=\dfrac{m}{3}\Rightarrow m=-2\)
Đúng 2
Bình luận (0)
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
Bài 2: Cho phương trình: x2 – 5x + m = 0 (m là tham số).
a) Giải phương trình trên khi m = 6.
b) Tìm m để phương trình trên có hai nghiệm x1, x2 phân biệt.
Giải thích các bước giải:
a.Với m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}
b.Để phương trình có 2 nghiệm x1,x2x1,x2
Đúng 1
Bình luận (0)
a, khi m=6 thì pt\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
b,Ta có:\(\Delta=\left(-5\right)^2-4.1.m=25-4m\)
để pt có 2 nghiệm x1, x2 phân biệt thì \(\Delta>0\) hay \(25-4m>0\Rightarrow m< \dfrac{25}{4}\)
Đúng 1
Bình luận (0)
Cho phương trình: x2 - 5x + m - 1 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm phân biệt x1;x2 sao cho: 2x2 = \(\sqrt{x_1}\)
\(\Delta=\left(-5\right)^2-4\left(m-1\right)\)
\(=25-4m+4\)
\(=29-4m\)
Để pt có 2 nghiệm thì \(\Delta>0\)
\(\Leftrightarrow m< \dfrac{29}{4}\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\) (1)
\(2x_2=\sqrt{x_1}\) ; \(ĐK:x_1;x_2\ge0\)
\(\Leftrightarrow4x_2^2=\left|x_1\right|\)
\(\Leftrightarrow4x_2^2=x_1\) (2)
Thế \(x_1=4x^2_2\) vào \(\left(1\right)\), ta được:
\(\left\{{}\begin{matrix}4x_2^2+x_2-5=0\\4x_2^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x_2=-\dfrac{5}{4}\left(ktm\right)\\x_2=1\left(tm\right)\end{matrix}\right.\\4.1^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=1\\m=5\end{matrix}\right.\)
\(\left(2\right)\Rightarrow x_1=4\)
Vậy \(\left\{{}\begin{matrix}m=5\\x_1=4\\x_2=1\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho phương trình x 2 - 3x + m - 5 = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn điều kiện x 1 ; x 2 =4
x 2 - 3x + m - 5 = 0
a = 1; b = -3; c = m – 5
Δ = b 2 - 4ac = - 3 2 - 4(m - 5) = 29 - 4m
Phương trình có 2 nghiệm phân biệt x 1 ; x 2 khi và chỉ khi
Δ > 0 ⇔ 29 - 4m > 0 ⇔ m < 29/4
Theo định lí Vi-et ta có:
x 1 ; x 2 = c/a = m - 5
Theo bài ra
x 1 ; x 2 = 4 ⇔ m - 5 = 4 ⇔ m = 9 (Không TMĐK m < 29/4)
Vậy không tồn tại m thỏa mãn đề bài.
Đúng 0
Bình luận (0)
Cho pt xã -4x4 m=0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức 2x1 + x2 = 1 Cho pt: 2x2 3x-2m +3 = 0 ("). Tìm m để phương trình (") có 2 nghiệm phân biệt x1, x2 thỏa mãn hệ thức x1/x2 + xz/x1 =3 Cho pt xã 4x - m + 3 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức x1-x2=7 Giải gấp chi tiết giúp e vs ạ
6. Biết rằng phương trình x 3 −3x 2 +3 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 a+2b.7. Cho đa thức P(x) 2x 4 −x 3 −5x 2 +5x−5. Gọi a,b, c là ba nghiệm phân biệt của đa thức Q(x) x 3 −3x+1. Tính P(a).P(b).P(c).8. Biết rằng phương trình P(x) x 3 +3x 2 −1 có ba nghiệm phân biệt a b c. Chứng minh rằng c a 2 +2a− 2,b c 2 +2c−2,a b 2 +2b−2.
Đọc tiếp
6. Biết rằng phương trình x 3 −3x 2 +3 = 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 = a+2b.
7. Cho đa thức P(x) = 2x 4 −x 3 −5x 2 +5x−5. Gọi a,b, c là ba nghiệm phân biệt của đa thức Q(x) = x 3 −3x+1. Tính P(a).P(b).P(c).
8. Biết rằng phương trình P(x) = x 3 +3x 2 −1 có ba nghiệm phân biệt a < b < c. Chứng minh rằng c = a 2 +2a− 2,b = c 2 +2c−2,a = b 2 +2b−2.
Cho phương trình x^2-3x-m+4=0
a) giải phương trình với m=6
b) tìm m để phương trình có nghiệm
C) tìm m để phương trình có hai nghiệm phân biệt x2,x2 biết x1+2x2=5
a, \(x^2-3x-6+4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
Ta có : \(\left(-3\right)^2-4.\left(-2\right)=9+8=17>0\)
Nên có 2 nghiệm phân biệt
\(x_1=\frac{3-\sqrt{17}}{2};x_2=\frac{3+\sqrt{17}}{2}\)
b, Để PT có nghiệm thì \(\Delta=0\)
\(\Leftrightarrow b^2-4ac=0\)
\(\Leftrightarrow\left(-3\right)^2-4\left(-m+4\right)=0\)
\(\Leftrightarrow9+4m-16=0\)
\(\Leftrightarrow7+4m=0\)
\(\Leftrightarrow m=-\frac{7}{4}\)
Vậy => m = -7/4
c, Ko rõ
Cho phương trình \(x^2-2mx+4m-6=0\) Tìm giá trị của tham số m để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn :
a) 0<x1<2<x2
b) 0<x1<x2<2
Phương trình
2
+
3
x
+
1
-
2
a
.
2
-
3
x
-
4
0
có 2 nghiệm phân biệt
x...
Đọc tiếp
Phương trình 2 + 3 x + 1 - 2 a . 2 - 3 x - 4 = 0 có 2 nghiệm phân biệt x 1 , x 2 , thỏa mãn x 1 - x 2 = log 2 + 3 3 . Khi đó a thuộc khoảng
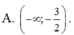
![]()