△ABC cân tại A, D trung điểm AH, D có tung độ dương, điểm I\(\left(\frac{11}{3};\frac{5}{3}\right)\) là tâm đường tròn ngoại tiếp △ABC; E\(\left(\frac{13}{3};\frac{5}{3}\right)\)trọng tâm △ADC. M(3;-1) thuộc DC, N(-3;0) thuộc AB. Tìm tọa độ A,B,C
Những câu hỏi liên quan
Trong mp hệ tọa độ oxy cho tam giác ABC có trực tâm H(3,0) và trung điểm của BC là điểm I(6,1). Đường thẳng AH có phương trình x+2y-3=0. Gọi D và E lần lượt là chân đường cao kẻ từ B và C của tam giác ABC. Xác định tọa độ biết rằng đường thẳng DẺ có pt: x-2=0 và D có tung độ dương
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH 12cm; BC 18cmBài 2: Cho tam giác ABC (AC AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:a, DE là đường trung trực của AHb, DEKH là hình thang cânBài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AHb, CM: AI vuôn...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD
Cho △ABC cân tại A, vẽ phân giác AH (H \(\in\) BC)
a) CM: △AHC = △AHB
b) Gọi I là trung điểm của HC. Qua I vẽ đường thẵng \(_{\perp}\) HC, đường thẳng này \(\cap\) AC tại D. CM △DHC cân tại D
c) Gọi G là giao điểm của AH và BD, M là trung điểm của AB. CM 2GM = GB
d) CM Chu vi △ABC > AH + 3CG
O x và y khác nhau ở điểm truc nên ta có phuong trình x +y bằng 65% tỉ lệ hành hóa
Đúng 0
Bình luận (0)
Tam giác ABC có góc ACB = 30 độ , Vẽ AH vuông góc với BC tại điểm H : AH = 1/2 BC , D là trung điểm của AB a, C/m: Tam giác ABC cân b, Tính góc BCD
a) Xét ∆ ABC có :
AH là đường cao đồng thời là trung tuyến
=> ∆ABC cân tại A
b) Vẽ E là trung điểm Kẻ CE
Vì ∆ABC cân tại A
=> AB = AC
=> ABC = ACB
Vì D là trung điểm AB
=> AD = DB
Vì E là trung điểm AC
=> AE = EC
=> AE = EC = AD = DB
Xét ∆ EBC và ∆ DCB ta có :
BC chung
CE = BD ( cmt)
ACB = ABC ( cmt)
=> ∆EBC = ∆DCB (c.g.c)
=> DCB = EBC ( tg ứng)
Mà ABC = ACB
=> ACD = ABE
Vì D là trung điểm AB
=> CD là trung tuyến AB
=> CD là phân giác ACB
Vì E là trung điểm AC
=> BE là trung tuyến AB
=> BE là phân giác ABC
=> DCB = ACD
=> ABE = EBC
=> DCB = 180° - \(\frac{1}{2}\)ACB - \(\frac{1}{2}\)ABC
Mà ACB = ABC = 30°
=> DCB = 180° - \(\frac{60°}{4}\)= 15°
Đúng 0
Bình luận (0)
bạn tự vẽ hình
a) tam giác vuông AHC có:
\(\widehat{C}=30^o\Rightarrow AH=\frac{1}{2}.AC\)(trong 1 t/g vuông, cạnh đối diện 1 góc 30 độ = 1 nửa cạnh huyền)
mà \(AH=\frac{1}{2}.BC\Rightarrow BC=AC\Rightarrow\Delta ABC\text{ cân tại }C\)
Vậy ...
Đúng 0
Bình luận (0)
??
câu b. Xét t/g ACD và t/g BCD, có:
AC=CB(t/g ABC cân tại C)
CAD^=CBD^ (t/g ABC cân tại C)
AD=BD( D là trung điểm của AB)
=> t/g ACD = t/g BCD (c.g.c)
=> ADC^=CDB^
Mà ADC^+CDB^=180o => CDB^=90o
Vậy góc BCD= 90 độ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A có H là trung điểm BC, O là trung điểm ACa) Chứng minh HO//AB và HO=1/2ABb) Lấy điểm D sao cho O là trung điểm HD, gọi I là trung điểm AH. Chứng minh B,I,D thẳng hàngc) Gọi HD cắt CI tại G. Chứng minh CD, BG, OI cùng cắt nhau tại 1 điểm
Xem chi tiết
a: Xét ΔABC có
H,O lần lượt là trung điểm của CB,CA
=>HO là đường trung bình của ΔABC
=>HO//AB và \(HO=\dfrac{AB}{2}\)
b: Ta có: HO//AB
O\(\in\)HD
Do đó: HD//AB
Ta có: HO=AB/2
HO=HD/2
Do đó: AB=HD
Xét tứ giác ABHD có
HD//AB
HD=AB
Do đó: ABHD là hình bình hành
=>AH cắt BD tại trung điểm của mỗi đường
mà I là trung điểm của AH
nên I là trung điểm của BD
=>B,I,D thẳng hàng
Đúng 2
Bình luận (0)
Cho đường thẳng (d): y=ax+b. Xác định các số nguyên a,b sao cho (d) đi qua điểm A(4;3) và cắt trục tung tại điểm có tung độ là một số nguyên dương, cắt trục hoành tại điểm có hoành độ là một số nguyên dương.
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.a, c/m: tam giác AHB tam giác AHCb, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IBID. c/m IBIC, từ đó suy ra AH+BD AB+ACc, Trên cạnh CI lấy điểm E sao cho CEfrac{2}{3}CI. c/m D,E,H thẳng hàngBài 2: Cho tam giác ABC có góc A 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: IDIE
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a, c/m: tam giác AHB = tam giác AHC
b, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB=ID. c/m IB=IC, từ đó suy ra AH+BD > AB+AC
c, Trên cạnh CI lấy điểm E sao cho CE=\(\frac{2}{3}\)CI. c/m D,E,H thẳng hàng
Bài 2: Cho tam giác ABC có góc A= 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: ID=IE
Tam giác ABC có góc ACB = 30 độ , Vẽ AH vuông góc với BC tại điểm H : AH = 1/2 BC , D là trung điểm của AB
a, C/m: Tam giác ABC cân
b, Tính góc BCD
Cho tam giác ABC cân tại A có góc A=120 độ, kẻ AH vuông góc BC tại H. Gọi D là trung điểm của AB, đường trung trực của AB cắt AB tại D và cắt BC tại E,. Chứng minh:tam giác BED = tam giác AEH
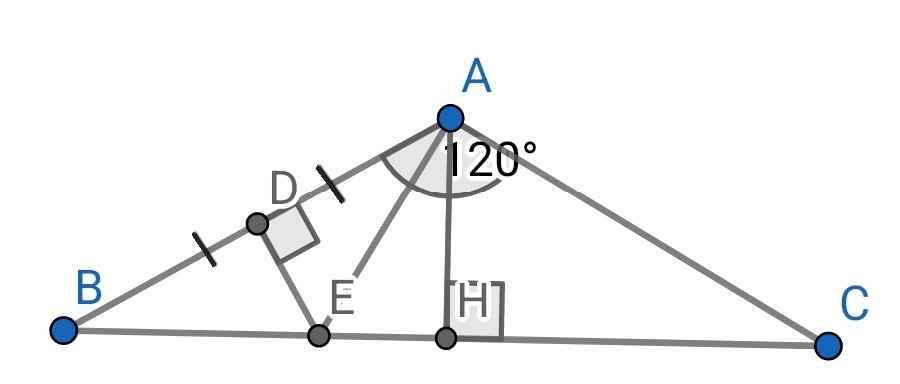Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
∆AHB vuông tại H (do AH ⊥ BC)
⇒ ∠B + ∠BAH = 90⁰
⇒ ∠BAH = 90⁰ - ∠B
= 90⁰ - 30⁰
= 60⁰
Xét hai tam giác vuông: ∆AED và ∆BED có:
ED là cạnh chung
AD = BD (do D là trung điểm của AB)
⇒ ∆AED = ∆BED (hai cạnh góc vuông)
⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)
⇒ ∠EAH = ∠BAH - ∠EAD
= 60⁰ - 30⁰
= 30⁰
⇒ ∠EAH = ∠EAD
Xét hai tam giác vuông: ∆AEH và ∆AED có:
AE là cạnh chung
∠EAH = ∠EAD = 30⁰
⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)
Mà ∆AED = ∆BED (cmt)
⇒ ∆BED = ∆AEH
Đúng 3
Bình luận (0)