Cho △ABC có A(-2;1), B(2;3), C(1;-5)
a. Viết phương trình các cạnh của ΔABC
b. Viết phương trình các đường trung tuyến của ΔABC
c. Viết phương trình các đường trung trực của ΔABC
d. Viết phương trình đường phân giác trong của góc A của ΔABC
Những câu hỏi liên quan
Câu 1:
1) Cho tam giác ABC có góc A = góc C-10độ; góc B=góc C + 10độ. Tính các góc của tam giác ABC?
2) Cho tam giác ABC có góc B= 7/6 góc C; góc A= 5/6 góc C. Tính các góc của tam giác ABC?
3) cho tam giác ABC có góc A= 2. Góc B ; góc B = góc C . tính các góc của tam giác ABC?
4) Cho tam giác ABC có góc A= 5.góc C; góc B= 2.góc C. tínhcác góc của tam giác ABC?
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
bài 1: cho tam giác ABC có A-B+C= 90 độ và A-C=-5 độ .So sánh cạnh trong tam giác ABC
Xem chi tiết
bài 2:cho tam giác ABC có A+B-2C=27 độ và A+3C=273 độ.So sánh các cạnh trong tam giác ABC
bài 3:cho tam giác ABC có C-3B-2A=-3 độ và 5B-2A=16 độ. Tính các góc từ đó so sánh các cạnh trong tam giác ABC
1 cho △ABC thỏa mãn: 2cos B= √2.Khi đó B=?2 cho △ABC có C^=45 độ,B^=75 độ số đo góc A là bao nhiêu3 cho △ABC có s=84,a=13,b=14,c=15 độ dài bán kính đường tròn ngoại tiếp r của △ trên là?
Xem chi tiết
1. \(2cosB=\sqrt{2}\Rightarrow cosxB=\dfrac{\sqrt{2}}{2}\Rightarrow B=45^0\)
2. \(A=180^0-\left(B+C\right)=60^0\)
3. \(r=\dfrac{S}{p}=\sqrt{3}\)
4. \(R=\dfrac{abc}{4S}=\dfrac{65}{8}\)
Đúng 0
Bình luận (0)
Câu 2 a. Cho tam giác ABC cân tại A có AB = 3cm. Tính độ dài cạnh AC ?
b) Cho tam giác ABC cân tại A có 
. Tính số đo góc C ?
1.Cho 2 tam giác bằng nhau ABC và MNP có A^ 50 độ và B^ 70 độ.Số đo góc C là bao nhiêu?2.Cho 2 tam giác ABC và MNP có A^ M^ 90 độ, B^ N^. Cần điều kiện gì để 2 tam giác ABC và MNP bằng nhau theo trường hợp cạnh góc vuông - góc nhọn?3.Cho tam giác ABC có góc A là góc tù,B^ C^.Trong các khẳng định sau khẳng định nào đúng?A.AB AC BCB.AC AB BCC.BC AB ACDBC AC AB4.Cho tam giác MNP có MN 5 cm , NP 4 cm , MP 6cm.Trong các khẳng định sau,khẳng định nào đúng?A. M^ N^ P^B.N^ P^ M^C.M^...
Đọc tiếp
1.Cho 2 tam giác bằng nhau ABC và MNP có A^ = 50 độ và B^ = 70 độ.Số đo góc C là bao nhiêu?2.Cho 2 tam giác ABC và MNP có A^ = M^ = 90 độ, B^ = N^. Cần điều kiện gì để 2 tam giác ABC và MNP bằng nhau theo trường hợp cạnh góc vuông - góc nhọn?3.Cho tam giác ABC có góc A là góc tù,B^ > C^.Trong các khẳng định sau khẳng định nào đúng?A.AB > AC > BC
B.AC > AB > BC
C.BC > AB > AC
D>BC > AC > AB4.Cho tam giác MNP có MN = 5 cm , NP = 4 cm , MP = 6cm.Trong các khẳng định sau,khẳng định nào đúng?A. M^ > N^ >P^
B.N^ > P^ > M^
C.M^ > P^ > N^
D.N^ > M^ > P^
Cho tam giác ABC cân tại A.Kẻ AD vuông góc với BC.Chứng minh rằng :a) Tam giác ADB = tam giác ADCb) AD là tia phân giác của góc A
Câu 1: Số đo góc C là 60 độ
Câu 2: Thiếu điều kiện AB=MN
Câu 3: Chọn C
Câu 4: Chọn B
Đúng 1
Bình luận (0)
cho \(\Delta ABC\) có A(1;-2) B(3;0) C(-2;-1). tính diện tích \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2,2\right)\\\overrightarrow{BC}=\left(-5,-1\right)\\\overrightarrow{AC}=\left(-3,1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{2^2+2^2}=2\sqrt{2}\\BC=\sqrt{\left(-5\right)^2+\left(-1\right)^1}=\sqrt{26}\\AC=\sqrt{\left(-3\right)^2+1^2}=\sqrt{10}\end{matrix}\right.\)
\(p=\dfrac{2\sqrt{2}+\sqrt{26}+\sqrt{10}}{2}\)
Áp dụng công thức Herong:
\(S=\sqrt{p.\left(p-2\sqrt{2}\right)\left(p-\sqrt{26}\right)\left(p-\sqrt{10}\right)}=\sqrt{16}=4\)
Đúng 1
Bình luận (0)
Câu 1: Cho tam giác ABC vuông tại A, có đường cao AH.a) Chứng minh Delta ABC tỉ lệ với Delta HACb)Chứng minh AC^2BC.CHCâu 2: Cho tam giác ABC vuông tại A, có đường cao AH. Biết HB4cm,HC9cm.a) Chứng minh: AH^2HB.HCb) Tính diện tích tam giác ABCCâu 3: Cho hình chữ nhật ABCD có AB8cm, BC6cm. Vẽ đường cao AH của Delta ADB a) Tính DBb) Chứng minh Delta ADH~Delta ADBc) Chứng minh AD^2DH.DBd) Chứng minh Delta AHB~Delta BCD Giúp mik vs ạ
Đọc tiếp
Câu 1: Cho tam giác ABC vuông tại A, có đường cao AH.
a) Chứng minh \(\Delta ABC\) tỉ lệ với \(\Delta HAC\)
b)Chứng minh \(AC^2\)=BC.CH
Câu 2: Cho tam giác ABC vuông tại A, có đường cao AH. Biết HB=4cm,HC=9cm.
a) Chứng minh: \(AH^2\)=HB.HC
b) Tính diện tích tam giác ABC
Câu 3: Cho hình chữ nhật ABCD có AB=8cm, BC=6cm. Vẽ đường cao AH của \(\Delta ADB\)
a) Tính DB
b) Chứng minh \(\Delta ADH~\Delta ADB\)
c) Chứng minh \(AD^2\)=DH.DB
d) Chứng minh \(\Delta AHB~\Delta BCD\)
Giúp mik vs ạ
2:
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
b: BC=4+9=13cm
AH=căn 4*9=6cm
S ABC=1/2*6*13=39cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC. A.
-
2
;
4
;
-
3
B.
6
;
0
;
5
C....
Đọc tiếp
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.
A. - 2 ; 4 ; - 3
B. 6 ; 0 ; 5
C. 0 ; 1 ; - 1 3
D. - 4 3 ; - 1 3 ; - 1
Đáp án C
Ta có: 
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
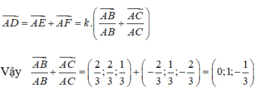
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.
Đúng 0
Bình luận (0)