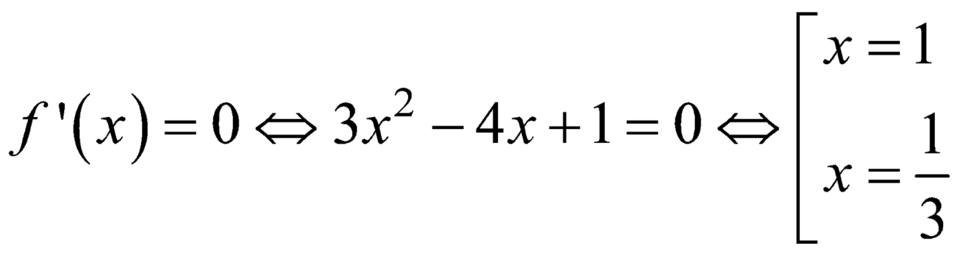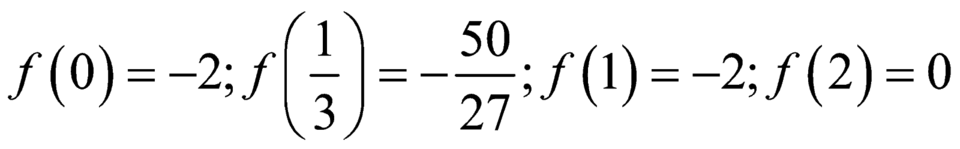Tìm GTNN của hàm số f(x)=2x2+\(\frac{3}{x}\) trên đoạn [\(\frac{1}{2}\);1]

Những câu hỏi liên quan
Câu 1: Cho hàm số : y = f(x) = 2x2 - 10
a) Tính f (0) ; f (1) ; f \(\left(-1\frac{1}{2}\right)\)
b) Tìm x biết f (x) = - 2
a/ Thay x =0 vào hàm số f(x) = 2x2 - 10 ta có
f(0) = 2 . 0 - 10 = -10
Thay x = 1 vào hàm số f(x) = 2x2 - 10 ta có
f(1) = 2 . 12 - 10 = 2 - 10 = -8
Thay \(x=-1\dfrac{1}{2}=-\dfrac{3}{2}\)vào hàm số f(x) ta có
\(f\left(-1\dfrac{1}{2}\right)=2.\left(-\dfrac{3}{2}\right)^2-10=\dfrac{9}{2}-\dfrac{20}{2}=-\dfrac{11}{2}\)
b/ f(x) = -2
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\Leftrightarrow x=\pm2\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
f
(
x
)
x
3
-
2
x
2
+
x
-
2
trên đoạn [0;2].
Đọc tiếp
Tìm giá trị lớn nhất của hàm số f ( x ) = x 3 - 2 x 2 + x - 2 trên đoạn [0;2].
![]()
![]()
![]()
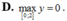
Tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x) = 2x2- ln( 3-4x) trên đoạn [ -2; 0]
A. Max y=8; min y=1-ln4
B. max y=8-ln11; miny=1/8 -ln4
C. max y=8+ln11; min y=-ln4
D. max y=8+ln 4; min y=4+ln11
Tìm giá trị lớn nhất của hàm số
y
f
(
x
)
x
3
-
2
x
2
+
x
-
2
trên đoạn [0;2] A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = f ( x ) = x 3 - 2 x 2 + x - 2 trên đoạn [0;2]
A. ![]()
B. 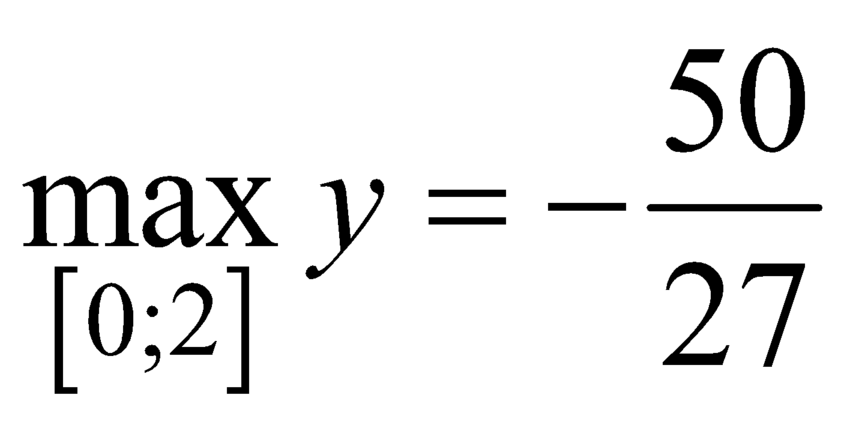
C. ![]()
D. ![]()
Tìm giá tị nhỏ nhất của hàm số sau trên đoạn [0;2] : \(f\left(x\right)=4x+\frac{3}{\left(x+1\right)^2}\)
\(f\left(x\right)=4x+\frac{3}{\left(x+1\right)^2}=2x+2+2x+2+\frac{3}{\left(x+1\right)^2}-4\ge3\sqrt[3]{\left(2x+2\right)^2.\frac{3}{\left(x+1\right)^2}}-4\)
\(=3\sqrt[3]{48}-4\)
Dấu \(=\)khi \(2x+2=\frac{3}{\left(x+1\right)^2}\Leftrightarrow\left(x+1\right)^3=\frac{3}{2}\Leftrightarrow x=\sqrt[3]{\frac{3}{2}}-1\).
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left(x\right)=\frac{x^2+x+1}{x+1}\) trên đoạn \(\left[\frac{1}{2};2\right]\)
Hàm số \(f\left(x\right)\) liên tục trên đoạn \(\left[\frac{1}{2};2\right]\)
+)\(f'\left(x\right)=\frac{x^2+2x}{\left(x+1\right)^2};f'\left(x\right)=0\Leftrightarrow x=0\notin\left[\frac{1}{2};2\right]\)hoặc \(x=-2\notin\left[\frac{1}{2};2\right]\)
+) \(f\left(\frac{1}{2}\right)=\frac{7}{6};f\left(2\right)=\frac{7}{3}\)
Vậy \(minf\left(x\right)_{x\in\left[\frac{1}{2};2\right]}=\frac{7}{6}\) khi \(x=\frac{1}{2}\)
\(maxf\left(x\right)_{x\in\left[\frac{1}{2};2\right]}=\frac{7}{3}\) khi \(x=2\)
Đúng 0
Bình luận (0)
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
2
+
1
trên
-
1
;
1
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
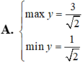
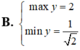
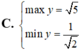
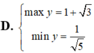
\(f\left(x;y;z\right)=\frac{x}{y}+\sqrt{\frac{y}{z}}+\sqrt[3]{\frac{z}{x}}\)
Tìm GTNN của hàm số đã cho
Áp dụng Bất Đẳng Thức Cauchy Schwardz ta được:
\(f\left(x;y;z\right)=6.\frac{\frac{x}{y}+\frac{1}{2}\sqrt{\frac{y}{z}}+\frac{1}{3}\sqrt[3]{\frac{z}{x}}+\frac{1}{3}\sqrt[3]{\frac{x}{z}}}{6}\)\(\ge6.\sqrt[6]{\frac{x}{y}.\frac{1}{2}\sqrt{\frac{y}{z}}.\frac{1}{2}\sqrt{\frac{y}{z}}.\frac{1}{3}\sqrt[3]{\frac{z}{x}}.\frac{1}{3}\sqrt[3]{\frac{z}{x}}}\)
\(=6.\sqrt{\frac{1}{2.2.3.3.3}\frac{x}{y}\frac{y}{z}\frac{z}{x}}=2^{2/3}.3^{1/2}\)
Vậy GTNN của \(f\left(x;y;z\right)=2^{2/3}.3^{1/2}\Leftrightarrow\frac{x}{y}=\frac{1}{2}\sqrt{\frac{y}{z}}=\frac{1}{3}\sqrt[3]{\frac{z}{x}}\)
Đúng 0
Bình luận (0)
bài 1: a/ cho hàm số yfrac{3}{2}x . điểm E ( -4;m ) là 1 điểm thuộc đồ thị của hàm số trên. tìm m. b/ cho hàm số yIm+frac{1}{2}I . x-3 đi qua điểm B ( 2;-1). c/ cho hàm số yf(x)(2a + 3).x + . tìm a biết f(1)-4bài 2: cho hàm số yf(x)-x^2+3x. tính f(-2), f(frac{2}{3}).
Đọc tiếp
bài 1: a/ cho hàm số \(y=\frac{3}{2}x\) . điểm E ( -4;m ) là 1 điểm thuộc đồ thị của hàm số trên. tìm m.
b/ cho hàm số y=I\(m+\frac{1}{2}\)I . x-3 đi qua điểm B ( 2;-1).
c/ cho hàm số y=f(x)=(2a + 3).x + . tìm a biết f(1)=-4
bài 2: cho hàm số y=f(x)=\(-x^2\)+3x. tính f(-2), f(\(\frac{2}{3}\)).
Cho hàm số f(x) = x4 - 2x2 + m - 1 (với m là tham số thực). Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số g(x) = \(\left|f\left(x\right)\right|\) trên đoạn [0;2] bằng 2020.
\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)
Đúng 0
Bình luận (0)