Bài 5

\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)

\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)

\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)

\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)

Xét tg ADE có

\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)

\(\Rightarrow Ax\perp Dy\)

Bài 6:

a/

Ta có

AB//CD => AB//DE

BE//AB (gt)

=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)

b/

CD - DE = CE

Mà AB = DE (cmt)

=> CD - AB = CE

c/

Xét tg BCE có

BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)

Mà CE = CD - DE và DE = AB (cmt) và BE = AD

=> BC+BE = BC + AD>CE = CD - AB

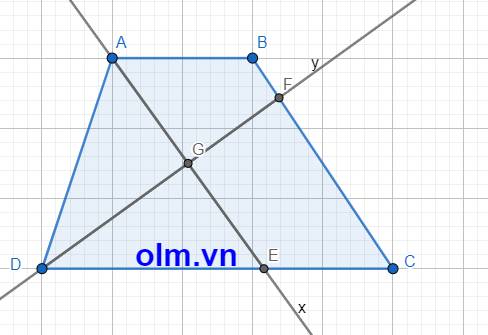
Gọi G là giao điểm của hai đường phân giác Ax và By 

Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)

           \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )

     ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\)) 

           \(\widehat{ADE}\) + \(\widehat{DAB}\) = 180⁰ (vì hai góc là hai góc trong cùng phía)

      ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 180⁰ = 90⁰

          Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 180⁰ (tổng ba góc trong 1 tam giác bằng 180⁰)

               ⇒ \(\widehat{DGA}\)  = 180⁰ - 90⁰ = 90⁰

Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)

AB = ?????? bao nhiêu hã bạn

a: Ta có: DC//AB

=>\(\hat{CDA}+\hat{DAB}=180^0\)

=>\(2\cdot\hat{DAB}+\hat{DAB}=180^0\)

=>\(3\cdot\hat{DAB}=180^0\)

=>\(\hat{DAB}=60^0\)

=>\(\hat{ADC}=2\cdot60^0=120^0\)

Ta có: ABCD là hình thang cân

=>\(\hat{CBA}=\hat{DAB}=60^0\) ; \(\hat{ADC}=\hat{DCB}=120^0\)

ΔCBA vuông tại C

=>\(\hat{CAB}+\hat{CBA}=90^0\)

=>\(\hat{CAB}=90^0-60^0=30^0\)

Ta có: tia AC nằm giữa hai tia AB và AD

=>\(\hat{DAC}+\hat{BAC}=\hat{DAB}\)

=>\(\hat{DAC}=60^0-30^0=30^0\)

Ta có: tia AC nằm giữa hai tia AD và AB

mà \(\hat{DAC}=\hat{BAC}\left(=30^0\right)\)

nên AC là phân giác của góc DAB

b: Ta có: \(\hat{DCA}=\hat{CAB}\) (hai góc so le trong, AB//CD)

\(\hat{DAC}=\hat{CAB}\)

Do đó: \(\hat{DCA}=\hat{DAC}\)

=>DA=DC=a

Ta có: ABCD là hình thang cân

=>DA=CB

=>CB=a

Kẻ DH⊥AB tại H và CK⊥AB tại K

Xét ΔDHA vuông tại H và ΔCKB vuông tại K có

DA=CB

\(\hat{DAH}=\hat{CBK}\)

Do đó: ΔDHA=ΔCKB

=>DH=CK và AH=BK

DH⊥AB

CK⊥AB

Do đó: DH//CK

Xét tứ giác DCKH có

DC//HK

DH//CK

Do đó: DCKH là hình bình hành

=>DC=HK=a

Gọi M là trung điểm của BC

Trên tia đối của tia MK, lấy I sao cho MK=MI

Xét tứ giác BKCI có

M là trung điểm chung của BC và KI

=>BKCI là hình bình hành

Hình bình hành BKCI có \(\hat{BKC}=90^0\)

nên BKCI là hình chữ nhật

=>BC=KI

mà \(KM=MI=\frac{KI}{2};MB=MC=\frac{BC}{2}\)

nên KM=MI=MB=MC=BC/2=KI/2

Xét ΔBMK có MK=MB và \(\hat{MBK}=60^0\)

nên ΔMBK đều

=>BK=MB=BC/2

=>BK=a/2

TA có: AB=AH+HK+KB

=a/2+a+a/2

=2a

Chu vi hình thang ABCD là:

AB+BC+CD+DA

=2a+a+a+a

=5a

ΔCKB vuông tại K

=>\(CK^2+KB^2=CB^2\)

=>\(CK^2=a^2-\left(\frac{a}{2}\right)^2=\frac{3a^2}{4}\)

=>\(CK=\frac{a\sqrt3}{2}\)

Diện tích hình thang BCDA là:

\(S_{DCBA}=\frac12\cdot CK\cdot\left(DC+BA\right)=\frac12\cdot\frac{a\sqrt3}{2}\cdot\left(a+2a\right)=\frac{a\sqrt3}{4}\cdot3a=3\sqrt3\cdot\frac{a^2}{4}\)