Cạnh huyền của một tam vuông cân bằng\(\sqrt{512}\) cm.Tính mỗi cạnh của tam giác đó.

Những câu hỏi liên quan
Cạnh huyền của một tam giác vuông cân bằng 49cm. Tính mỗi cạnh góc vuông của tam giác đó.
Gọi độ dài cạnh góc vuông của tam giác đó là a
Theo định lí Pitago :
a2 + a2 = 492
=> 2a2 = 2401
=> a2 = 2401 : 2 = 1200.5
=> a = \(\frac{49\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
ta có: tam giác ABC vuông cân tại A
=> AB = AC ( định lí) => AB2 = AC2
Xét tam giác ABC vuông tại A
=> AB2 + AC2 = 492 ( py-ta-go)
AB2 + AB2 = 492
2.AB2 = 492
AB2 = 1200,5
\(\Rightarrow AB=\sqrt{1200,5}cm\)
=> \(AB=AC=\sqrt{1200,5}cm\)
Đúng 0
Bình luận (0)
Cạnh huyền của 1 tam giác vuong cân bằng \(\sqrt{98cm}\).Tính mỗi gó vuông của tam giác vuông đó
a ) Tính độ dài cạnh huyền của một tam giác vuông cân biết cạnh góc vuông bằng 5 cm b) Tính độ dài cạnh góc vuông của một tam giác vuông cân biết cạnh huyền bằng 2 2
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụngm giác là tam giác cân.(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông câ...
Đọc tiếp
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụng
m giác là tam giác cân.
(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.
(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau
(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?
(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông cân. (7) Nêu các tính chất của tam giác đều. c) Đố bạn nêu chính xác các tính chất sau: (1) Nếu ba cạnh của tam giác này .... tam giác kia, thì hai tam giác đó bằng
(2) Nếu hai cạnh và góc xen giữa của tam giác này .... tam giác kia, thì giác đó bằng nhau.
(3) Nếu một cạnh và hai góc kề của tam giác này .... tam giác kia, thì hai ta đó bằng nhau.
(4) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vụ .... tam giác vuông kia, thì hai tam giác đó bằng nhau.
(5) Nếu cạnh huyền và một góc nhọn của tam giác vuông này .... tam giá kia, thì hai tam giác đó bằng nhau. | (6) Nếu hai cạnh góc vuông của tam giác vuông này .... tam giác vuông ki tam giác đó bằng nhau.
6 tính chất tam giác vuông cân
(7) Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này .... vuông kia, thì hai tam giác đó bằng nhau.
(8) Trong một tam giác vuông, bình phương của cạnh huyền bằng... cạnh g (9) Nếu một tam giác có bình phương của một cạnh bằng... đó là tam gi
Cứng minh đẳng thức sau : Trong một tam giác vuông bình phương mỗi cạnh góc vuông bằng cạnh huyền nhân với hình chiếu của cạnh đó lên cạnh huyền.( không dùng tam giác đồng dạng)
Bài 8: Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3:4 và chu vi tam giác là 36cm
Bài 9: Tính độ dài cạnh góc vuông của một tam giác vuông cân biết cạnh huyền bằng:
a) 2m b) 10m
Bài 10: Một tam giác vuông có cạnh huyền bằng 52cm, độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
Bài 11: Cho tam giác ABC cân tại B, AB17cm, AC 16cm. Gọi M là trung điểm của AC. Tính BM.
CÁc bạn giúp mình nhé....
Đọc tiếp
Bài 8: Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3:4 và chu vi tam giác là 36cm
Bài 9: Tính độ dài cạnh góc vuông của một tam giác vuông cân biết cạnh huyền bằng:
a) 2m b) 10m
Bài 10: Một tam giác vuông có cạnh huyền bằng 52cm, độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
Bài 11: Cho tam giác ABC cân tại B, AB=17cm, AC =16cm. Gọi M là trung điểm của AC. Tính BM.
CÁc bạn giúp mình nhé. Cảm ơn các bạn
Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé
Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c
Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)
\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)
Vì tam giác vuông nên ta theo pytago ta có: a2 + b2 = c2 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)
⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3
a = 3.3 = 9 (cm)
b = 3.4 = 12 (cm)
c = 3.5 = 15 (cm)
Kết luận: độ dài cạnh bé của góc vuông là: 9 cm
dộ dài cạnh lớn của góc vuông là 12 cm
độ dài cạnh huyền là 15 cm
Đúng 0
Bình luận (0)
Bài 8: Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3:4 và chu vi tam giác là 36cm
Bài 9: Tính độ dài cạnh góc vuông của một tam giác vuông cân biết cạnh huyền bằng:
a) 2m b) 10m
Bài 10: Một tam giác vuông có cạnh huyền bằng 52cm, độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
Bài 11: Cho tam giác ABC cân tại B, AB17cm, AC 16cm. Gọi M là trung điểm của AC. Tính BM.
CÁc bạn giúp mình nhé....
Đọc tiếp
Bài 8: Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3:4 và chu vi tam giác là 36cm
Bài 9: Tính độ dài cạnh góc vuông của một tam giác vuông cân biết cạnh huyền bằng:
a) 2m b) 10m
Bài 10: Một tam giác vuông có cạnh huyền bằng 52cm, độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
Bài 11: Cho tam giác ABC cân tại B, AB=17cm, AC =16cm. Gọi M là trung điểm của AC. Tính BM.
CÁc bạn giúp mình nhé. Cảm ơn các bạn
Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
Đúng 0
Bình luận (0)
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48
Đúng 0
Bình luận (0)
Bài 11
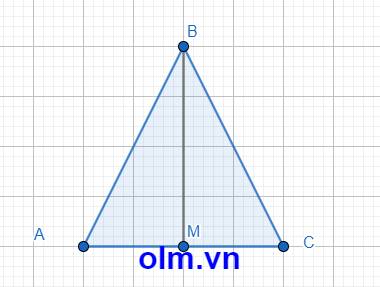
AM = \(\dfrac{1}{2}\) AC ( vì M là trung điểm AC)
AM = 16 \(\times\) \(\dfrac{1}{2}\) = 8 (cm)
BM \(\perp\)AC ( vì trong tam giác cân đường trung tuyến cũng là đường cao, đường trung trực)
⇒\(\Delta\)MAB vuông tại M
Xét tam giác vuông MAB theo pytago ta có:
AB2 = AM2 + BM2
⇒ BM2 = AM2 - AM2 = 172 - 82 = 225
BM = \(\sqrt{225}\) cm = 15 cm
Kết luận BM = 15 cm
Đúng 0
Bình luận (0)
Bài 1 Các câu sau đúng Đ hay sai S 1 Tam giác có 2 góc bằng 45° là tam giác vuông cân.2 Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau3 Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau4 Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.5 Tam giác cân có 1 góc bằng 60° là tam giác đều.6 Tạm giác cân có 1 góc bằng 45...
Đọc tiếp
Bài 1 Các câu sau đúng Đ hay sai S 1 Tam giác có 2 góc bằng 45° là tam giác vuông cân.2 Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau3 Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau4 Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.5 Tam giác cân có 1 góc bằng 60° là tam giác đều.6 Tạm giác cân có 1 góc bằng 45° là tam giác vuông cân.7 Nếu tam giác có độ dài 3 cạnh lần lượt là 3,4,5 thì tam giác đó là tam giác vuông.8 Hai tam giác đều thì bằng nhau.9 Góc ngoài của tam giác luôn lớn hơn mỗi góc trong của tam giác đó.10 Trong tam giác cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực củacạnh đáy.11 Nếu cạnh huyền của tam giác vuông cân này bằng cạnh huyền của tam giác vuông cânkia thì 2 tam giác đó bằng nhau .12 Tam giác ABC vuông tại A, M là trung điểm của đoạn thắng BC. Nếu AB 2 cm, AC 51 cm thì AM 2 cm.13 Tam giác ABC vuông tại A, M là trung điểm của BC. Nếu 2B 30° và AM 6 cm, thìAC 6cm.14 Nếu 2 tam giác cân có 2 cặp cạnh bên bằng nhau thì 2 tam giác cân đó bằng nhau.15 Nếu cạnh bên và cạnh đáy của tam giác cân này bằng cạnh bên và cạnh đáy của tam giáccân kia thì 2 tam giác cân bằng nhau.16 Nếu 2 tam giác cân có chung góc ở đỉnh thì 2 cạnh đáy của chúng song song với nhau.17 Nếu 2 cạnh và 1 góc của tam giác này lần lượt bằng 2 cạnh và 1 góc của tam giác kia thì2 tam giác đó bằng nhau.18 Nếu 3 tam giác cân AMN , BMN , CMN cùng chung cạnh đáy MN thì 3 điểm A, B, Cthắng hàng.19 Nếu 2 tam giác vuông cân có 1 cặp cạnh góc vuông bằng nhau thì chúng bằng nhau.20 Trong tam giác cân các góc đều có thể là góc nhọn hoặc góc tù.
một tam giác vuông cạnh huyền bằng 20cm và tổng 2 cạnh góc vuông bằng 28cm. Tính mỗi cạnh của tam giác vuông


















