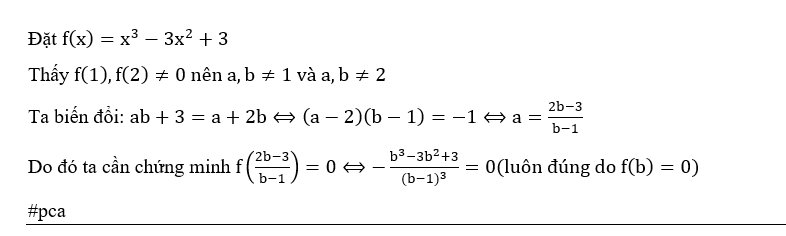1.

Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)

\(f\left(x\right)\) xác định và liên tục trên R

\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)

\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)

\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)

\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)

\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)

\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)

\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)

\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)

Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt

2.

Đặt \(t=g\left(x\right)=x.cosx\)

\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)

\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)

Hàm \(f\left(t\right)\) xác định và liên tục trên R

\(f\left(1\right)=1>0\)

\(f\left(-2\right)=-8< 0\)

\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m

3. Chắc ngoặc thứ là \(\left(2m^2-2m+4040\right)\) ?

\(\Leftrightarrow\left(m^2-m+2021\right)x^3-2\left(m^2-m+2020\right)x^2-4x+m^2-m+2021=0\)

Do \(m^2-m+2020>0\), đặt \(m^2-m+2020=n^2\)

\(\Rightarrow\left(n^2+1\right)x^3-2n^2x^2-4x+n^2+1=0\)

Quy về bài số 1

Đặt \(f\left(x\right)=\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)\)

Hàm \(f\left(x\right)\) hiển nhiên liên tục trên R

Do vai trò a;b;c như nhau, không mất tính tổng quát giả sử \(a< b< c\)

\(f\left(a\right)=\left(a-b\right)\left(a-c\right)\)

\(f\left(b\right)=\left(b-a\right)\left(b-c\right)\)

\(f\left(c\right)=\left(c-a\right)\left(c-b\right)\)

\(f\left(a\right).f\left(b\right)=\left(a-b\right)\left(a-c\right)\left(b-a\right)\left(b-c\right)=\left(a-b\right)^2\left(c-a\right)\left(b-c\right)\)

Do \(a< b< c\Rightarrow\left\{{}\begin{matrix}c-a>0\\b-c< 0\end{matrix}\right.\) \(\Rightarrow f\left(a\right).f\left(b\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (a;b)

\(f\left(b\right).f\left(c\right)=\left(b-a\right)\left(b-c\right)\left(c-a\right)\left(c-b\right)=\left(b-c\right)^2\left(a-b\right)\left(c-a\right)\)

Do \(a< b< c\Rightarrow\left\{{}\begin{matrix}a-b< 0\\c-a>0\end{matrix}\right.\) \(\Rightarrow f\left(b\right).f\left(c\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (b;c)

Vậy pt đã cho luôn có 2 nghiệm phân biệt

a) Xét \(\Delta=\left(m+1\right)^2-2m+3=m^2+4>0,\forall m\)

Vậy PT luôn có 2 nghiệm phân biệt.

b) \(f\left(x\right)=x^2-\left(m+1\right)x+2m-3=0\)có nghiệm \(x=3\)khi và chỉ khi

\(f\left(3\right)=0\Leftrightarrow3^2-\left(m+1\right).3+2m-3=0\Leftrightarrow3-m=0\Leftrightarrow m=3\)

Xét pt cho là pt bậc hai một ẩn $x$ ( Với $a=1 \neq 0, b=-2(m-1), c = m-3$ )

Ta có : \(\Delta'=b'^2-ac\)

\(=\left[-\left(m-1\right)\right]^2-\left(m-3\right)\cdot1\)

\(=m^2-2m+1-m+3\)

\(=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\)

Nên pt cho luôn có hai nghiệm phân biệt \(\forall m\)