Trong mặt phẳng Oxy cho (d1) : y = 2x-7 ; (d2) : y = -x-1.
a) Vẽ (d1),(d2)
b) Tìm tọa độ giao điểm của (d1) và (d2)
c) Viết phương trình đường thẳng (d3) song song với (d2) và cắt đường thẳng (d1) tại một điểm nằm trên trục tung.

Những câu hỏi liên quan
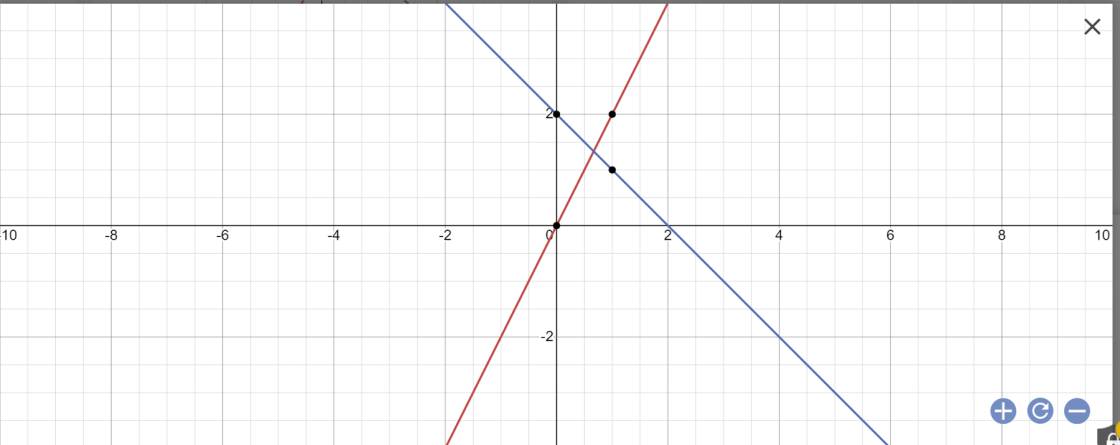
trong mặt phẳng tọa độ oxy cho đường thẳng (d1) y=2x và đường thẳng (d2) y=-x+2 a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ
Lập bảng giá trị:
| x | 2 | 0 | -2 |
| y=2x | 4 | 0 | -4 |
| y=-x+2 | 0 | 2 | 4 |
Vẽ đồ thị:
Đúng 1
Bình luận (0)
trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1): y2x+4 (d2): y-x+4, (dm): y (m+3)x-7(m≠3)1) Xác định giá trị m để đường thẳng (dm) // với đường thẳng (d1)2) Xác định giá trị của m để đường thẳng (d1) và đường thẳng (d2) trên cùng mặt phẳng tọa độ Oxy3)Gọi A và B lần lượt là giao điểm của đường thẳng (d1) và đường thẳng (d2) với trục Ox. Tìm tọa độ các điểm A và B5) Tính diện tích tam giác ABC (đơn vị các trục tọa độ cm)
Đọc tiếp
trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1): y=2x+4 (d2): y=-x+4, (dm): y= (m+3)x-7(m≠3)
1) Xác định giá trị m để đường thẳng (dm) // với đường thẳng (d1)
2) Xác định giá trị của m để đường thẳng (d1) và đường thẳng (d2) trên cùng mặt phẳng tọa độ Oxy
3)Gọi A và B lần lượt là giao điểm của đường thẳng (d1) và đường thẳng (d2) với trục Ox. Tìm tọa độ các điểm A và B
5) Tính diện tích tam giác ABC (đơn vị các trục tọa độ cm)
1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng
d
1
:
2
x
-
4
y
-
3
0
và
d
2
:
3
x
-
y
+
17
0
. Số đo góc giữa
d
1
và
d
2
là A.
45...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d 1 : 2 x - 4 y - 3 = 0 và d 2 : 3 x - y + 17 = 0 . Số đo góc giữa d 1 và d 2 là
A. 45 °
B. 90 °
C. 30 °
D. 60 °
Trong mặt phẳng Oxy cho 2 đường thẳng d1: 2x - y + 5=0, d2: 3x + 6y - 7=0. Lập phương trình đường thẳng đi qua P (2; -1) sao cho đường thẳng đó cắt d1, d2 tạo ra một tam giác cân có đỉnh là giao điểm của d1, d2
d1 có 1 vtpt là \(\overrightarrow{n1}\)(2;-1);d2 có 1 vtpt là \(\overrightarrow{n2}\)(3;6)
Ta có \(\overrightarrow{n1}\)\(\times\)\(\overrightarrow{n2}\)=2\(\times\)3-1\(\times\)6=0 nên d1 vuông góc d2 và d1 cắt d2 tại I(I khác P)
Gọi d là đườg thẳng đi qua P;d:A(x-2)+B(y+1)=0\(\Leftrightarrow\)Ax+By-2A+B=0
d cắt d1;d2 tạo thành một tam giác cân có đỉnh I\(\Leftrightarrow\)d tạo với d1(hoặc d2) một góc 45
\(\Leftrightarrow\)\(\frac{\left|2A-B\right|}{\sqrt{A^2+B^2}\sqrt{2^2+\left(-1\right)^2}}\)=\(\cos45\)
\(\Leftrightarrow\)\(3A^2\)-8AB-\(3B^2\)=0
\(\Leftrightarrow\)A=3B hoặc B=-3A
Nếu A=3B ta có d:3x+y-5=0
Nếu B=-3A to có d:x-3y-5=0
Vậy......
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng
d
1
:
y
2
x
−
3
y
+
1
0
và
d
2
:
x
+
y
−
2
0.
Có bao nhiêu phép tịnh tiến biến
d
1
thành
d...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d 1 : y = 2 x − 3 y + 1 = 0 và d 2 : x + y − 2 = 0. Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A. Vô số
B. 0
C. 1
D. 4
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng
d
1
:
2
x
+
3
y
+
1
0
và
d
2
:
x
-
y
-
2
0
Có bao nhiêu phép tịnh tiến biến...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0
và d 2 : x - y - 2 = 0 Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A.Vô số
B.4
C.1
D.0
Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2
Đúng 0
Bình luận (0)
Câu 2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d1):y=2x và đường thẳng (d2):y=-x+2. a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Cho đường thẳng (d3):y=ax+b Xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2) đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1.
a: 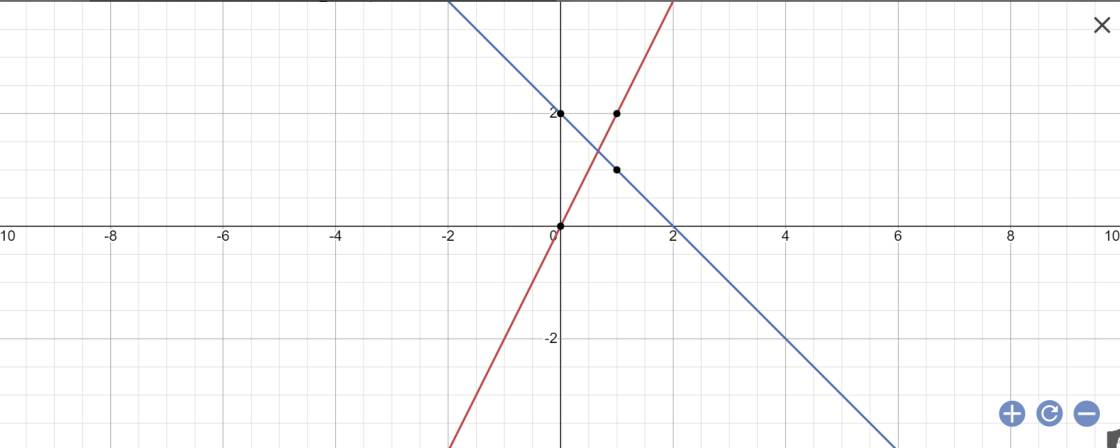
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
\(b-1=2\)
=>b=2+1=3
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa đô Oxy cho đường thẳng d1 y=x và d2 y=-2x+4
a. Vẽ d1 và d2
b. Cho đưởng thẳng d3 y=ã+b xác dịnh a b biết d3 song song với d1 và cắt trục hoành tại hoành độ bằng 2
trong mặt phẳng oxy viết phương trình đường tròn (c) có tâm nằm trên trục hoành và đường tròn (c) tiếp xúc với cả hai đường thẳng (d1):2x-y-1=0 (d2):x-2y+1=0 Trong mặt phẳng Oxy,viết phương trình đường tròn
Trong mặt phẳng toạ độ Oxy cho (d):y=3x+m-2 Tìm m để (d) cắt (d1):y=-2x+6m+3 tại một điểm thuộc đường tròn (O) bán kính là 3
Lời giải:
PT hoành độ giao điểm:
$3x+m-2=-2x+6m+3$
$\Leftrightarrow 5x=5m+5$
$\Leftrightarrow x=m+1$
$y=3x+m-2=3(m+1)+m-2=4m+1$
Vậy tọa độ giao điểm của $(d)$ và $(d_1)$ là $I(m+1, 4m+1)$
$I$ thuộc đường tròn $(O)$ bán kính 3
Tức là $OI=3$
$\Leftrightarrow \sqrt{(m+1)^2+(4m+1)^2}=3$
Giải pt trên suy ra $m=-1$ hoặc $m=\frac{7}{17}$
Đúng 0
Bình luận (0)






 help me pls
help me pls









