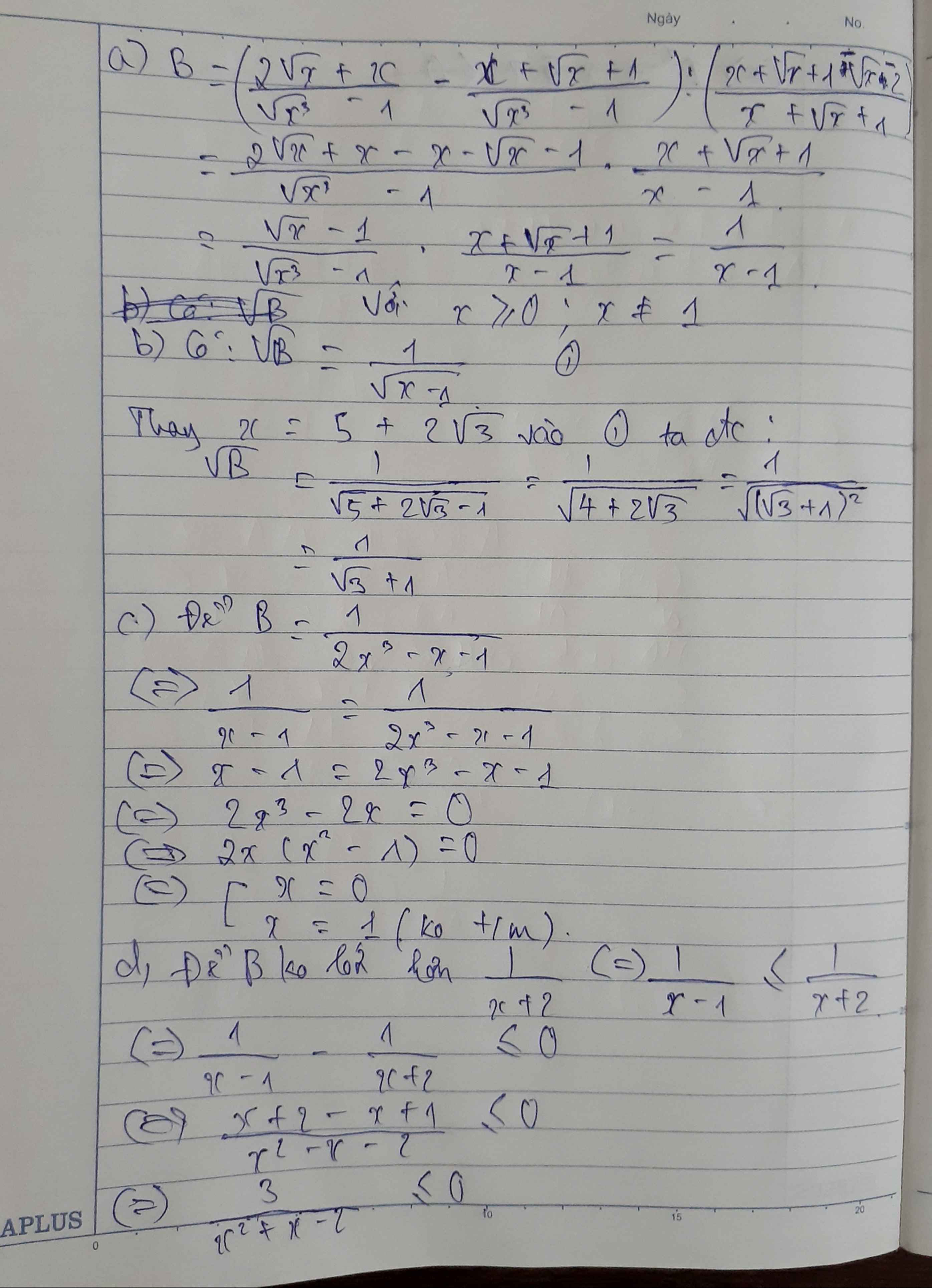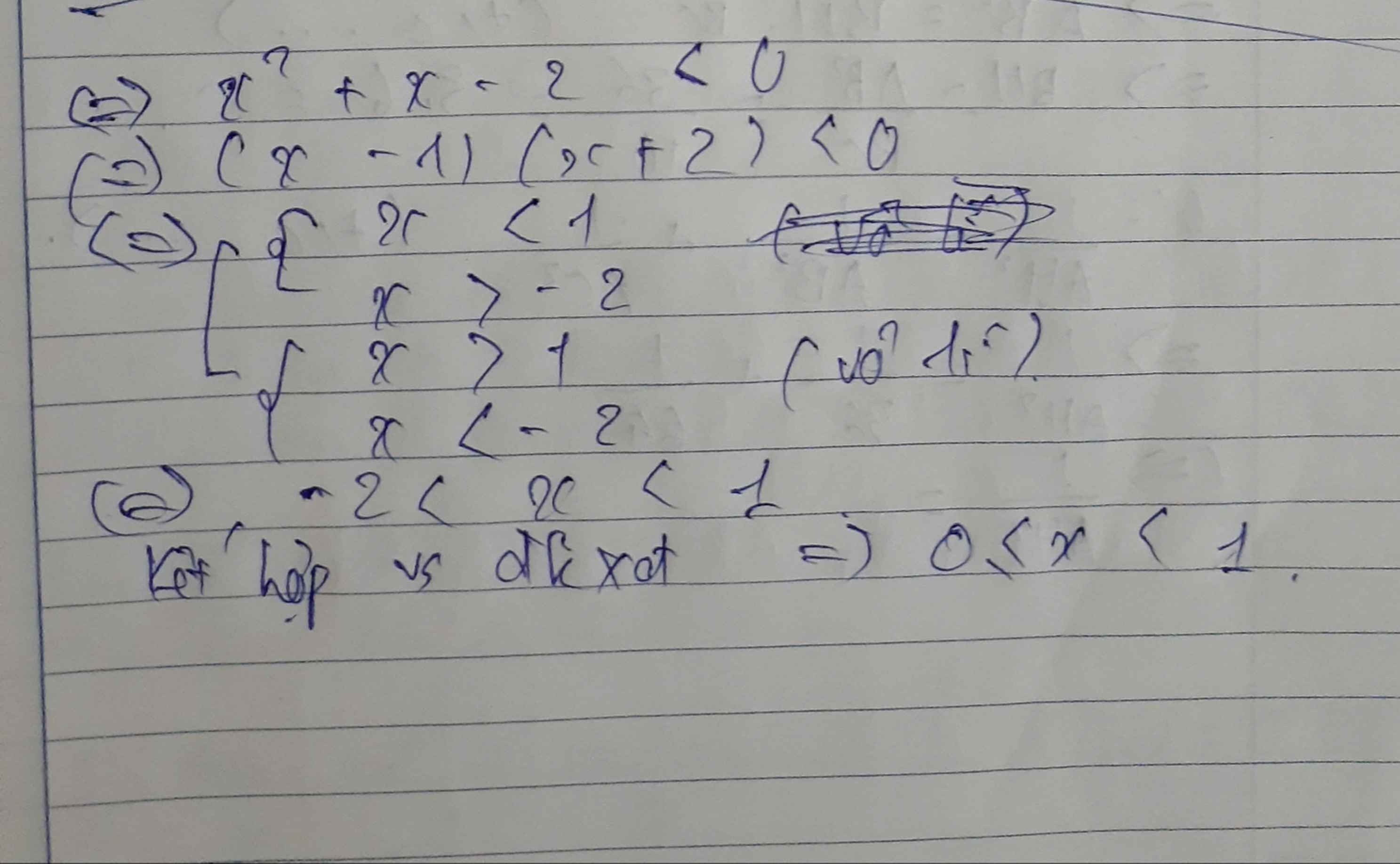tính giá trị bt \(\sqrt{5-2x}\) khi x = \(3\sqrt{2}-3\)

Những câu hỏi liên quan
Cho \(x=\frac{1}{2}\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}\) Tính giá trị BT
\(A=\left(4x^5+4x^4-x^3+1\right)^{2018}+\left(\sqrt{4x^5+4x^4-5x^3+3}\right)^3+\left(\frac{1-\sqrt{2}x}{\sqrt{2x^2+2x}}\right)\)tại giá trị x
cho bt A=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left[\dfrac{2}{x}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right]\)
a)rút gọn bt A
b)tính giá trị của bt A khi\(x=4+2\sqrt{3}\)
c)tìm giá trị của x để bt \(\sqrt{A}\)có giá trị nỏ nhất
ĐKXĐ: \(x>0;x\ne1\)
\(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+2\sqrt{x}\right).x.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+2\sqrt{x}\right)}=\dfrac{x}{\sqrt{x}-1}\)
b.
\(x=4+2\sqrt{3}=\left(\sqrt{3}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{3}+1\)
\(\Rightarrow A=\dfrac{4+2\sqrt{3}}{\sqrt{3}+1-1}=\dfrac{4+2\sqrt{3}}{\sqrt{3}}=\dfrac{6+4\sqrt{3}}{3}\)
c.
Để \(\sqrt{A}\) xác định \(\Rightarrow\sqrt{x}-1>0\Rightarrow x>1\)
Ta có:
\(\sqrt{A}=\sqrt{\dfrac{x}{\sqrt{x}-1}}=\sqrt{\dfrac{x}{\sqrt{x}-1}-4+4}=\sqrt{\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4}\ge\sqrt{4}=2\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=0\Rightarrow x=4\)
Đúng 0
Bình luận (1)
Cho A=\(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}vaB=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\)
a)tính giá trị của bt A khi x=2
b)rút gọn bt B
c) tìm x sao cho bt P=-A.B nhận giá trị là số nguyên
tính giá trị của bt
P=\(\frac{\sqrt{x^3+x^2+5x+3}+6}{\sqrt{x^3-2x^2-7x+3}}\) tại x=1+\(\sqrt[3]{2}+\sqrt[3]{4}\)
P (dfrac{2}{sqrt{x}-1}-dfrac{5}{x+sqrt{x}-2}):(1+dfrac{3-x}{left(sqrt{x}-1right).left(sqrt{x}+2right)}
a) rút gọn bt (làm mỗi ý này thôi cũng đc ạ)
b) Tính P khi x6-2sqrt{5}
c) Tìm giá trị của x để P dfrac{1}{sqrt{x}}
d) Tìm x thuộc Z để P thuộc Z
e) Tìm x để P 1-sqrt{x}
g) Tìm min P
Đọc tiếp
P= (\(\dfrac{2}{\sqrt{x}-1}\)-\(\dfrac{5}{x+\sqrt{x}-2}\)):(1+\(\dfrac{3-x}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+2\right)}\)
a) rút gọn bt (làm mỗi ý này thôi cũng đc ạ)
b) Tính P khi x=6-2\(\sqrt{5}\)
c) Tìm giá trị của x để P= \(\dfrac{1}{\sqrt{x}}\)
d) Tìm x thuộc Z để P thuộc Z
e) Tìm x để P< 1-\(\sqrt{x}\)
g) Tìm min P
a:
ĐKXĐ: x>=0; x<>1
Ta có: \(\frac{2}{\sqrt{x}-1}-\frac{5}{x+\sqrt{x}-2}\)
\(=\frac{2}{\sqrt{x}-1}-\frac{5}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{2\left(\sqrt{x}+2\right)-5}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\frac{2\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
Ta có: \(1+\frac{3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)+3-x}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+2\right)}\)
\(=\frac{x+\sqrt{x}-2+3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
Ta có: \(P=\left(\frac{2}{\sqrt{x}-1}-\frac{5}{x+\sqrt{x}-2}\right):\left(1+\frac{3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right)\)
\(=\frac{2\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}:\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{2\sqrt{x}-1}{\sqrt{x}+1}\)
b: Thay \(x=6-2\sqrt5=\left(\sqrt5-1\right)^2\) vào P, ta được:
\(P=\frac{2\cdot\sqrt{\left(\sqrt5-1\right)^2}-1}{\sqrt{\left(\sqrt5-1\right)^2}+1}\)
\(=\frac{2\left(\sqrt5-1\right)-1}{\sqrt5-1+1}=\frac{2\sqrt5-3}{\sqrt5}=2-\frac{3}{\sqrt5}=2-\frac{3\sqrt5}{5}=\frac{10-3\sqrt5}{5}\)
c: \(P=\frac{1}{\sqrt{x}}\)
=>\(\frac{2\sqrt{x}-1}{\sqrt{x}+1}=\frac{1}{\sqrt{x}}\)
=>\(2x-\sqrt{x}=\sqrt{x}+1\)
=>\(2x-2\sqrt{x}-1=0\)
=>\(x-\sqrt{x}-\frac12=0\)
=>\(x-\sqrt{x}+\frac14-\frac34=0\)
=>\(\left(\sqrt{x}-\frac12\right)^2=\frac34\)
=>\(\left[\begin{array}{l}\sqrt{x}-\frac12=\frac{\sqrt3}{2}\\ \sqrt{x}-\frac12=-\frac{\sqrt3}{2}\end{array}\right.\Rightarrow\left[\begin{array}{l}\sqrt{x}=\frac{\sqrt3+1}{2}\\ \sqrt{x}=\frac{-\sqrt3+1}{2}\left(loại\right)\end{array}\right.\)
=>\(\sqrt{x}=\frac{\sqrt3+1}{2}\)
=>\(x=\left(\frac{\sqrt3+1}{2}\right)^2=\frac{4+2\sqrt3}{4}=\frac{2+\sqrt3}{2}\)
d: Để P là số nguyên thì \(2\sqrt{x}-1\) ⋮\(\sqrt{x}+1\)
=>\(2\sqrt{x}+2-3\) ⋮\(\sqrt{x}+1\)
=>-3⋮\(\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\lbrace1;3\right\rbrace\)
=>\(\sqrt{x}\in\left\lbrace0;2\right\rbrace\)
=>x∈{0;4}
e: \(P<1-\sqrt{x}\)
=>\(\frac{2\sqrt{x}-1}{\sqrt{x}+1}<1-\sqrt{x}\)
=>\(2\sqrt{x}-1<\left(1-\sqrt{x}\right)\left(\sqrt{x}+1\right)=-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=-\left(x-1\right)=-x+1\)
=>\(2\sqrt{x}-1+x-1<0\)
=>\(x+2\sqrt{x}+1-3<0\)
=>\(\left(\sqrt{x}+1\right)^2<3\)
=>\(\sqrt{x}+1<\sqrt3\)
=>\(\sqrt{x}<\sqrt3-1\)
=>\(x<4-2\sqrt3\)
Kết hợp ĐKXĐ, ta được: 0<=x<\(4-2\sqrt3\)
Đúng 0
Bình luận (0)
a:
ĐKXĐ: x>=0; x<>1
Ta có: \(\frac{2}{\sqrt{x}-1}-\frac{5}{x+\sqrt{x}-2}\)
\(=\frac{2}{\sqrt{x}-1}-\frac{5}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{2\left(\sqrt{x}+2\right)-5}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\frac{2\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
Ta có: \(1+\frac{3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)+3-x}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+2\right)}\)
\(=\frac{x+\sqrt{x}-2+3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
Ta có: \(P=\left(\frac{2}{\sqrt{x}-1}-\frac{5}{x+\sqrt{x}-2}\right):\left(1+\frac{3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right)\)
\(=\frac{2\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}:\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{2\sqrt{x}-1}{\sqrt{x}+1}\)
b: Thay \(x=6-2\sqrt5=\left(\sqrt5-1\right)^2\) vào P, ta được:
\(P=\frac{2\cdot\sqrt{\left(\sqrt5-1\right)^2}-1}{\sqrt{\left(\sqrt5-1\right)^2}+1}\)
\(=\frac{2\left(\sqrt5-1\right)-1}{\sqrt5-1+1}=\frac{2\sqrt5-3}{\sqrt5}=2-\frac{3}{\sqrt5}=2-\frac{3\sqrt5}{5}=\frac{10-3\sqrt5}{5}\)
c: \(P=\frac{1}{\sqrt{x}}\)
=>\(\frac{2\sqrt{x}-1}{\sqrt{x}+1}=\frac{1}{\sqrt{x}}\)
=>\(2x-\sqrt{x}=\sqrt{x}+1\)
=>\(2x-2\sqrt{x}-1=0\)
=>\(x-\sqrt{x}-\frac12=0\)
=>\(x-\sqrt{x}+\frac14-\frac34=0\)
=>\(\left(\sqrt{x}-\frac12\right)^2=\frac34\)
=>\(\left[\begin{array}{l}\sqrt{x}-\frac12=\frac{\sqrt3}{2}\\ \sqrt{x}-\frac12=-\frac{\sqrt3}{2}\end{array}\right.\Rightarrow\left[\begin{array}{l}\sqrt{x}=\frac{\sqrt3+1}{2}\\ \sqrt{x}=\frac{-\sqrt3+1}{2}\left(loại\right)\end{array}\right.\)
=>\(\sqrt{x}=\frac{\sqrt3+1}{2}\)
=>\(x=\left(\frac{\sqrt3+1}{2}\right)^2=\frac{4+2\sqrt3}{4}=\frac{2+\sqrt3}{2}\)
d: Để P là số nguyên thì \(2\sqrt{x}-1\) ⋮\(\sqrt{x}+1\)
=>\(2\sqrt{x}+2-3\) ⋮\(\sqrt{x}+1\)
=>-3⋮\(\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\lbrace1;3\right\rbrace\)
=>\(\sqrt{x}\in\left\lbrace0;2\right\rbrace\)
=>x∈{0;4}
e: \(P<1-\sqrt{x}\)
=>\(\frac{2\sqrt{x}-1}{\sqrt{x}+1}<1-\sqrt{x}\)
=>\(2\sqrt{x}-1<\left(1-\sqrt{x}\right)\left(\sqrt{x}+1\right)=-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=-\left(x-1\right)=-x+1\)
=>\(2\sqrt{x}-1+x-1<0\)
=>\(x+2\sqrt{x}+1-3<0\)
=>\(\left(\sqrt{x}+1\right)^2<3\)
=>\(\sqrt{x}+1<\sqrt3\)
=>\(\sqrt{x}<\sqrt3-1\)
=>\(x<4-2\sqrt3\)
Kết hợp ĐKXĐ, ta được: 0<=x<\(4-2\sqrt3\)
Đúng 0
Bình luận (0)
1. cho biểu thức
A=\(\dfrac{\sqrt{x}-1}{x^2-x}:\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right)\)
a. rứt gọn
b, tính giá trị của bt A khi x=4+\(2\sqrt{3}\)
a, \(A=\dfrac{\sqrt{x}-1}{x^2-x}:\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right)=\dfrac{\sqrt{x}-1}{x\left(\sqrt{x}\pm1\right)}:\left(\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{1}{x\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{1}=1\)
Đúng 1
Bình luận (0)
b, Cho A = 1 rồi còn gì, hay đề lỗi bạn ?
\(x=4+2\sqrt{3}=\sqrt{3}^2+2\sqrt{3}+1=\left(\sqrt{3}+1\right)^2\)
\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)
xem là bài mình làm có sai đâu ko nhé nếu rút gọn ra kq khác thì thay bên trên vào nhé
Đúng 0
Bình luận (1)
a) Ta có: \(A=\dfrac{\sqrt{x}-1}{x^2-x}:\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right)\)
\(=\dfrac{\sqrt{x}-1}{x\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{1}\)
=1
Đúng 0
Bình luận (0)
\(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\) và \(B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}-\dfrac{4}{1-\sqrt{x}}+\dfrac{5-x}{x-1}\left(x\ge0;x\ne1\right)\)
a,Tính giá trị của A khi x = 9
b,Rút gọn BT P = A.B
mọi người giúp mình với :((
a:Thay x=9 vào A, ta được:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
cho Bleft(dfrac{2sqrt{x}+x}{xsqrt{x}-1}-dfrac{1}{sqrt{x}-1}right)divleft(1-dfrac{sqrt{x}+2}{x+sqrt{x}+1}right)a. rút gọn Bb. tính sqrt{B} khi x5+2sqrt{3}c. tìm x để B dfrac{1}{2x^3-x-1}d. tìm giá trị của x để giá trị của B không lớn hơn giá trị biểu thức dfrac{1}{x+2}Lm nhanh giúp mk nhé mk đang cần gấp
Đọc tiếp
cho B=\(\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right)\div\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
a. rút gọn B
b. tính \(\sqrt{B}\) khi \(x=5+2\sqrt{3}\)
c. tìm x để B= \(\dfrac{1}{2x^3-x-1}\)
d. tìm giá trị của x để giá trị của B không lớn hơn giá trị biểu thức \(\dfrac{1}{x+2}\)
Lm nhanh giúp mk nhé mk đang cần gấp
a) \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{x-1}=\dfrac{1}{x-1}\)
Đúng 1
Bình luận (0)
a) Ta có: \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x+\sqrt{x}+1}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{1}{x-1}\)
Đúng 0
Bình luận (0)
cho 2 bt A=\(\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\) và B=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right):\dfrac{x+16}{\sqrt{x}+2}\)
Tính giá trị của A khi x=36
Rút gọn bt B
Hãy tìm các giá trị của x nguyên để giá trị của biểu thức B(A-1) là số nguyên
a: Thay x=36 vào A, ta được:
\(A=\frac{\sqrt{36}+4}{\sqrt{36}+2}=\frac{6+4}{6+2}=\frac{10}{8}=\frac54\)
b: \(B=\left(\frac{\sqrt{x}}{\sqrt{x}+4}+\frac{4}{\sqrt{x}-4}\right):\frac{x+16}{\sqrt{x}+2}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-4\right)+4\left(\sqrt{x}+4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\frac{\sqrt{x}+2}{x+16}\)
\(=\frac{x-4\sqrt{x}+4\sqrt{x}+16}{x-16}\cdot\frac{\sqrt{x}+2}{x+16}=\frac{\sqrt{x}+2}{x-16}\)
c: Đặt P=B(A-1)
\(=\frac{\sqrt{x}+2}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\left(\frac{\sqrt{x}+4}{\sqrt{x}+2}-1\right)\)
\(=\frac{\sqrt{x}+2}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\frac{2}{\sqrt{x}+2}=\frac{2}{x-16}\)
Để P là số nguyên thì 2⋮x-16
=>x-16∈{1;-1;2;-2}
=>x∈{17;15;18;14}
Đúng 0
Bình luận (0)