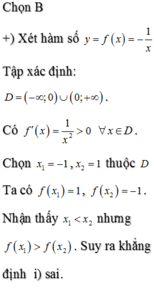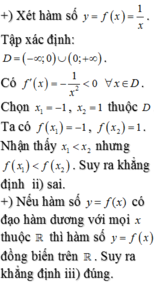Cho hàm số y = f(x) = 1/2x.
chứng tỏ rằng x1 > x2 thì f(x1) > f(x2)
cảm ơn vì đã giải nha :) :)

Những câu hỏi liên quan
Cho hàm số y=F(x)=1/2x.Chứng minh rằng nếu : X1>X2 thì F(X1)>F(X2)
Giúp e vs ạk
Cho hàm số y=f(x)=2x-3. X lấy giá trị thực bất kì x1, x2 sao cho x1 < x2. Chứng tỏ f(x1) < f(x2). Kết luận về tính biến thiên của hàm số
b1 : Viết công thức của hàm số y = f(x) biết rằng y tỉ lệ thuận vs x theo hệ số tỉ lệ \(\frac{1}{4}\)
a) Tìm x để f(x) = -5
b) cmr : nếu x1 > x2 thì f(x1) > f(x2)
b2 : Viết công thức của hàm số y = f(x) biết rằng y tỉ lệ nghịch vs x theo hệ số a = 12 .
a) f(10x) = 10f(x)
b) f(x1+x2) = f(x1)+f(x2)
c) f(x1 - x2 ) = f(x1) - f(x2)
Viết công thức của hàm số y = f(x) biết rằng y tỷ lệ thuận với x theo hệ số tỷ lệ a/ Tìm x để f(x) = -5 b/ Chứng tỏ rằng nếu x1> x 2 thì f(x1) > f(x2)
Cho hàm số y = f(x) = kx (k là hằng số, k ( 0). Chứng minh rằng:
a/ f(10x) = 10f(x)
b/ f(x1 + x2) = f(x1) + f(x2)
c/ f(x1 - x2) = f(x1) - f(x2)
Bài 4 : Cho hàm số y = f(x) = kx (k là hằng số, k ( 0). Chứng minh rằng:
a/ f(10x) = 10f(x)
b/ f(x1 + x2) = f(x1) + f(x2)
c/ f(x1 - x2) = f(x1) - f(x2)
a. ta có \(f\left(10x\right)=k.10x=10.kx=10f\left(x\right)\)
b. \(f\left(x_1+x_2\right)=k\left(x_1+x_2\right)=kx_1+kx_2=f\left(x_1\right)+f\left(x_2\right)\)
c.\(f\left(x_1-x_2\right)=k\left(x_1-x_2\right)=kx_1-kx_2=f\left(x_1\right)-f\left(x_2\right)\)
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm dương với mọi x thuộc tập số D thì
f
x
1
f
x
2
∀
x
1
,
x
2
∈
D
,
x
1
x
2
ii) Nếu hàm số yf(x) có đạo hàm âm với...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc tập số D thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
ii) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc tập số D thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
iii) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc R thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
iv) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc R thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
Số khẳng định đúng là
A. 1
B. 2
C. 3
D. 4
cho hàm số y=f(x)có tính chất f(x1.x2)=f(x1).f(x2) chứng minh rằng
f(1)=1
Cho hàm số y f(x) 3x.Cho x hai giá trị bất kì
x
1
,
x
2
sao cho
x
1
x
2
Hãy chứng minh
f
(
x
1
)
f
(
x
2
)
rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Đọc tiếp
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
Hãy chứng minh f ( x 1 ) < f ( x 2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho x các giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
= > x 1 - x 2 < 0
Ta có:
f x 1 = 3 x 1 ; f x 2 = 3 x 2 ⇒ f x 1 − f x 2 = 3 x 1 − 3 x 2 = 3 x 1 − x 2 < 0 ⇒ f x 1 < f x 2
Vậy với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Đúng 0
Bình luận (0)