Tìm giao điểm K của Ox với Ac

Những câu hỏi liên quan
1)Tam giác ABC có AB30cm, AC40cm. Trên tia đối của tia AC lấy điểm D sao cho ADAB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC.2) Tam giác ABC có ABAC. Gọi d là đường trung trực của BC, E là giao điểm của d với AC. Gọi K là một điểm bất kì thuộc d (K khác E). So sánh chu vi các tam giác AKB và AEB.3) Cho điểm A nằm trong góc nhọn xOy. Vẽ điểm D đối xứng với A qua Ox. Vẽ điểm E đối xứng với A qua Oy. Gọi B và C theo thứ tự là gi...
Đọc tiếp
1)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC.
2) Tam giác ABC có AB<AC. Gọi d là đường trung trực của BC, E là giao điểm của d với AC. Gọi K là một điểm bất kì thuộc d (K khác E). So sánh chu vi các tam giác AKB và AEB.
3) Cho điểm A nằm trong góc nhọn xOy. Vẽ điểm D đối xứng với A qua Ox. Vẽ điểm E đối xứng với A qua Oy. Gọi B và C theo thứ tự là giao điểm của DE với Ox và Oy. Chứng minh rằng tam giác ABC có chu vi nhỏ nhất trong các tam giác có một đỉnh là A, hai đỉnh kia nằm trên các tia Ox và Oy.
)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC
Đúng 0
Bình luận (0)
kẻ AB vuông góc dot o i Ox(B in O X ) . AC vuông góc với Oy(C in Oy) . a) Chứng minh :\ CO=: Delta ABO 7a 1,7 225 c) Gọi K là giao điểm của tia Oy với đường thăng AB, H là giao điểm tia Cho góc xOy nhọn .A là một điểm thuộc tia phân giác của góc đó.Từ A, b)Tam giác ABC là tam giác gì.Vì sao? Chứng minh : hat AHK = hat AKH | | Ox với đường thẳng AC.
Đề lỗi quá nhiều x ngược
Mời bạn đăng lại câu hỏi
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD. Điểm M lần lượt thuộc các cạnh BC và SD. a) Tìm giao điểm I của BN với (SAC), và giao điểm J của MN với (SAC) b) DM cắt AC tại K .CMR;S,K,J thẳng hàng
Xem thêm câu trả lời
cho tứ diện SABC.Gọi H,K lần lượt là 2 điểm trên cạnh SA,SC sao cho HK không song song với AC. I là trung điểm BC
a) tìm giao điểm của SB và mp(ABC)
b) tìm giao điểm của HB và mp(SAC)
c) tìm giao điểm của BK và mp(SAC)
d) tìm giao điểm của HK và mp(ABC)
a) Để tìm giao điểm của đường thẳng SB và mặt phẳng (ABC), chúng ta cần tìm điểm giao nhau của đường thẳng SB và mặt phẳng (ABC). Điểm này sẽ nằm trên cả hai đường thẳng SB và mặt phẳng (ABC). Để tìm điểm này, ta có thể sử dụng phương pháp giao điểm giữa đường thẳng và mặt phẳng. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (ABC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng AB và AC, ví dụ như vector AB và vector AC. Sau đó, ta tìm phương trình đường thẳng SB, có thể được xác định bằng cách sử dụng hai điểm S và B. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng SB và phương trình mặt phẳng (ABC) để tìm điểm giao nhau.
b) Tương tự, để tìm giao điểm của đường thẳng HB và mặt phẳng (SAC), ta có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (SAC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng SA và SC, ví dụ như vector SA và vector SC. Sau đó, ta tìm phương trình đường thẳng HB, có thể được xác định bằng cách sử dụng hai điểm H và B. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng HB và phương trình mặt phẳng (SAC) để tìm điểm giao nhau.
c) Để tìm giao điểm của đường thẳng BK và mặt phẳng (SAC), ta cũng có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (SAC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng SA và SC, ví dụ như vector SA và vector SC. Sau đó, ta tìm phương trình đường thẳng BK, có thể được xác định bằng cách sử dụng hai điểm B và K. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng BK và phương trình mặt phẳng (SAC) để tìm điểm giao nhau.
d) Tương tự, để tìm giao điểm của đường thẳng HK và mặt phẳng (ABC), ta có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (ABC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng AB và AC, ví dụ như vector AB và vector AC. Sau đó, ta tìm phương trình đường thẳng HK, có thể được xác định bằng cách sử dụng hai điểm H và K. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng HK và phương trình mặt phẳng (ABC) để tìm điểm giao nhau.
Đúng 0
Bình luận (1)
cho tứ diện SABC.Gọi H,K lần lượt là 2 điểm trên cạnh SA,SC sao cho HK không song song với AC. I là trung điểm BC
a) tìm giao điểm của SB và mp(ABC)
b) tìm giao điểm của HB và mp(SAC)
c) tìm giao điểm của BK và mp(SAC)
d) tìm giao điểm của HK và mp(ABC)
Để tìm giao điểm của SB và mp(ABC), ta cần tìm giao điểm của hai đường thẳng SB và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng ABC. Vì I là trung điểm BC, ta có thể xác định được mặt phẳng ABC. Sau đó, ta tìm giao điểm của đường thẳng SB và mặt phẳng ABC.
Để tìm giao điểm của HB và mp(SAC), ta cần tìm giao điểm của hai đường thẳng HB và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng SAC. Tương tự như trên, ta xác định được mặt phẳng SAC và sau đó tìm giao điểm của đường thẳng HB và mặt phẳng SAC.
Để tìm giao điểm của BK và mp(SAC), ta cần tìm giao điểm của hai đường thẳng BK và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng SAC. Tương tự như trên, ta xác định được mặt phẳng SAC và sau đó tìm giao điểm của đường thẳng BK và mặt phẳng SAC.
Để tìm giao điểm của HK và mp(ABC), ta cần tìm giao điểm của hai đường thẳng HK và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng ABC. Tương tự như trên, ta xác định được mặt phẳng ABC và sau đó tìm giao điểm của đường thẳng HK và mặt phẳng ABC.
Đúng 0
Bình luận (0)
cho góc nhọn xoy gọi I là điểm thuộc tia phân giác của góc xoy kẻ ia vuông góc với ox kẻ ib vuông góc với oy gọi K là giao điểm của BI với OX gọi m là giao điểm của AI với OY chứng minh AB song song với MK
Bn viết rĩ hơn đc k
ngu\(\hept{\begin{cases}3\\3\end{cases}\hept{\begin{cases}5\\5\\5\end{cases}}5555555b5b5b55b}\)
cho mình hỏi câu này cho (d):1) với m -3 : a) vẽ đồ thị h/số trên b) tìm tọa độ giao điểm của (d) với (d2) : y 2x - 1 c) gọi A,B lần lượt là giao của (d) với Ox,Oy . tính Soab d) tính k/c từ 0 đến (d) 2) tìm m biết đồ thị h//số (d) đi qua điểm M (1,2)3) tìm m biết đồ thị h/số (d) cắt trục trung tại điểm có trung độ bằng 14) cho (d2) : y x + 5 ; (d3) : y -x - 2 tìm m để 3 đường thẳng (d),(d2),(d3) đồng quy
Đọc tiếp
cho mình hỏi câu này
cho (d):
1) với m = -3 : a) vẽ đồ thị h/số trên b) tìm tọa độ giao điểm của (d) với (d2) : y = 2x - 1 c) gọi A,B lần lượt là giao của (d) với Ox,Oy . tính Soab d) tính k/c từ 0 đến (d)
2) tìm m biết đồ thị h//số (d) đi qua điểm M (1,2)
3) tìm m biết đồ thị h/số (d) cắt trục trung tại điểm có trung độ bằng 1
4) cho (d2) : y = x + 5 ; (d3) : y = -x - 2 tìm m để 3 đường thẳng (d),(d2),(d3) đồng quy
cho (d):1) với m -3 : a) vẽ đồ thị h/số trên b) tìm tọa độ giao điểm của (d) với (d2) : y 2x - 1 c) gọi A,B lần lượt là giao của (d) với Ox,Oy . tính Soab d) tính k/c từ 0 đến (d) 2) tìm m biết đồ thị h//số (d) đi qua điểm M (1,2)3) tìm m biết đồ thị h/số (d) cắt trục trung tại điểm có trung độ bằng 14) cho (d2) : y x + 5 ; (d3) : y -x - 2 tìm m để 3 đường thẳng (d),(d2),(d3) đồng quy
Đọc tiếp
cho (d):
1) với m = -3 : a) vẽ đồ thị h/số trên b) tìm tọa độ giao điểm của (d) với (d2) : y = 2x - 1 c) gọi A,B lần lượt là giao của (d) với Ox,Oy . tính Soab d) tính k/c từ 0 đến (d)
2) tìm m biết đồ thị h//số (d) đi qua điểm M (1,2)
3) tìm m biết đồ thị h/số (d) cắt trục trung tại điểm có trung độ bằng 1
4) cho (d2) : y = x + 5 ; (d3) : y = -x - 2 tìm m để 3 đường thẳng (d),(d2),(d3) đồng quy
Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC , M là một điểm tùy ý trên cạnh AD.a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và IM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ).
Đọc tiếp
Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC , M là một điểm tùy ý trên cạnh AD.
a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)
b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và IM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).
c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ).
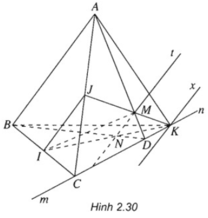
a)
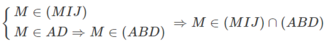
Ta cũng có:
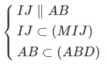
⇒ (MIJ) ∩ (ABD) = d = Mt và Mt // AB // IJ
b) Ta có: Mt // AB ⇒ Mt ∩ BD = N
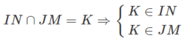
Vì K ∈ IN ⇒ K ∈ (BCD)
Và K ∈ JM ⇒ K ∈ (ACD)
Mặt khác (BCD) ∩ (ACD) = CD do đó K ∈ CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)
c) Ta có:
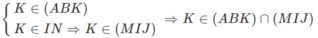
Mà
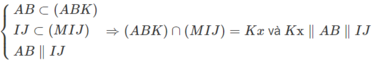
Đúng 0
Bình luận (0)





















