Tính diện tích tam giác giới hạn bởi các đường y = x; y = - x và y = 4.

Những câu hỏi liên quan
Cho hai đường thẳng y=x+1 và y=3-x.Tính diện tích tam giác giới hạn bởi hai đường thẳng trên trục Ox
Tính diện tích hình phẳng giới hạn bởi các đường : y= x3- x và y= x- x2
A.12/9
B. 37/12
C.32/7
D.25/8
Đồ thị hàm số y = x3 - x; y = x - x2 .Đặt f1(x) = x3 - x, f2(x) = x - x2
Ta có f1(x) - f2(x) = 0 <=> x3 + x2 - 2x = 0 có 3 nghiệm x = -2; x = 0 ; x = 1
Vậy : Diện tích hình phẳng đã cho là :
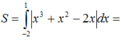
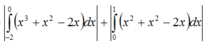
= 37 12
Đúng 0
Bình luận (0)
Tính diện tích giới hạn bởi các đường cong y (x - 1)lnx và y x - 1. A.
e
2
-
4
e
+
5
4
B.
3
e
2
-
2
e
+...
Đọc tiếp
Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.
A. e 2 - 4 e + 5 4
B. 3 e 2 - 2 e + 5 2
C. 7 e 2 - e + 2 3
D. 4 e 2 + 3 e - 2 5
Chọn A.
+) Xét phương trình: (x - 1)lnx = x - 1 ⇔ x = 1 hoặc x = e.
+ ) Diện tích cần tìm là:
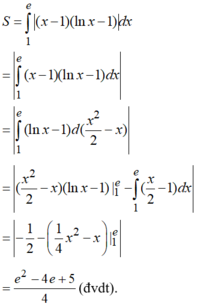
Đúng 0
Bình luận (0)
Tính diện tích giới hạn bởi các đường cong y(e+1)x; y (ex + 1)x A.
e
5
-
19
100
B.
2
e
3
-
73
50
C.
e
3
-
11
20
D.
e...
Đọc tiếp
Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (ex + 1)x
A. e 5 - 19 100
B. 2 e 3 - 73 50
C. e 3 - 11 20
D. e 2 - 1
Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = ( 1 + e x ) x <=> x = 0 hoặc x =1
Diện tích cần tính là S = ∫ 0 1 x e x d x - ∫ 0 1 e x d x = ∫ 0 1 x d ( e x ) - e ∫ 0 1 x d x
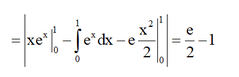
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng được giới hạn bởi các đường
x
y
2
;
y
x
3
;
y
x
A
.
1
2
B
.
1
4
C
.
2
3...
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi các đường x = y 2 ; y = x 3 ; y = x
A . 1 2
B . 1 4
C . 2 3
D . 1 3
Tính diện tích của hình giới hạn bởi các đường yx2-2 và
y
-
x
A. 13/3 B. 7/3 C.
13
π
3
D.
13
π
3
Đọc tiếp
Tính diện tích của hình giới hạn bởi các đường y=x2-2 và y = - x
A. 13/3
B. 7/3
C. 13 π 3
D. 13 π 3
Cho tam giác giới hạn bởi ba đường y=x, x=1 và trục Ox. Tính thể tích khối tròn xoay được tạo bởi phép quay tam giác đó quanh trục Oy.
A. π 3
B. 2 π 3
C. π
D. 4 π 3
Chọn B
Thể tích hình cần tính bằng thể tích khối trụ trừ đi thể tích khối nón
Đúng 0
Bình luận (0)
Cho tam giác giới hạn bởi ba đường y x, x 1 và trục Ox. Tính thể tích khối tròn xoay được tạo bởi phép quay tam giác đó quanh trục Oy. A.
π
3
B.
2
π
3
C.
π
D.
4
π
3
Đọc tiếp
Cho tam giác giới hạn bởi ba đường y = x, x = 1 và trục Ox. Tính thể tích khối tròn xoay được tạo bởi phép quay tam giác đó quanh trục Oy.
A. π 3
B. 2 π 3
C. π
D. 4 π 3
Chọn B
Thể tích hình cần tính bằng thể tích khối trụ trừ đi thể tích khối nón.
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi các đường sau: y xsin2x, y 2x,
x
π
2
A.
π
2
4
-
4
B.
π
2
-
π
C.
π
2
4
-
π...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x, x = π 2
A. π 2 4 - 4
B. π 2 - π
C. π 2 4 - π 4
D. π 2 4 + π 4
/
Chọn C.
Phương trình hoành độ giao điểm: x sin 2x = 2x <=> x (sin2x-2) = 0 <=> x = 0 hoặc sin2x = 2 (VN)
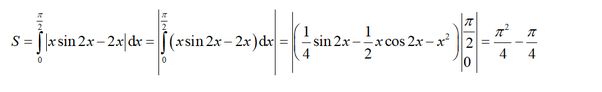
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = 2x – x 2 , x + y = 2






