Hoành độ Giao điểm chính là nghiệm của D=P vậy ta xem nó có bao nhiêu nghiệm

x^2=2x+m-3

(x-1)^2=m-4

Nếu m=4 => có một nghiệm x=1 có 1 giao điểm 

nếu m<4 => không tồn tại x => không có giao điểm

m>4 => \(\orbr{\begin{cases}x=1-\sqrt{m-4}\\x=1+\sqrt{m-4}\end{cases}}\) => có 2 điểm

Thank you

Xét pt: \(x^2-2mx+m^2-2m+3=0\) (1)

\(\Delta'=m^2-\left(m^2-2m+3\right)=2m-3\) 

- Nếu \(2m-3< 0\Leftrightarrow m< \dfrac{3}{2}\Rightarrow\left(1\right)\) vô nghiệm hay hàm xác định trên R

- Nếu \(2m-3=0\Leftrightarrow m=\dfrac{3}{2}\Rightarrow\left(1\right)\) có nghiệm kép \(x=\dfrac{3}{2}\) hay TXĐ của hàm: \(D=R\backslash\left\{\dfrac{3}{2}\right\}\)

- Nếu \(2m-3>0\Leftrightarrow m>\dfrac{3}{2}\Rightarrow\left(1\right)\) có 2 nghiệm pb \(x_{1,2}=m\pm\sqrt{2m-3}\) hay TXĐ của hàm là: \(D=R\backslash\left\{m-\sqrt{2m-3};m+\sqrt{2m-3}\right\}\)

Số giao điểm của ( C m ) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:

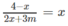
Ta có:

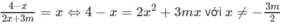
⇔ 2 x 2  + (3m + 1)x – 4 = 0 ⇔ 2 x 2  + (3m + 1) x – 4 = 0 với x ≠ −3m/2

    +) Thay x = −3m/2 vào (*), ta có:

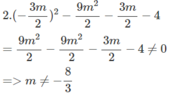
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m  ≠  −8/3.

Ta có: ∆ = 3 m + 1 2  + 32 > 0, ∀ m. Từ đó suy ra với m  ≠ −8/3 đường thẳng y = x luôn cắt ( C m ) tại hai điểm phân biệt.