GIải Phương trình nghiệm nguyên:
x2 +y2-xy=x+y+2
giải phương trình nghiệm nguyên:
x2-x=y2-1
Giải phương trình nghiệm nguyên:
x2-y2=1998
https://hoc24.vn/cau-hoi/chung-minh-rang-phuong-trinh-sau-khong-co-nghiem-nguyena-x2-y21998b-x2y21994.262907021445
y2 = x2 - 1998
x2 = 1998 + y2
y = \(\sqrt{x^2-1998}\)
x = \(\sqrt{1998+y^2}\)
y = x - \(\sqrt{1998}\)
x = y + \(\sqrt{1998}\)
giải phương trình nghiệm nguyên: x+y+xy=x2+y2
\(x+y+xy=x^2+y^2\)
⇔ \(2xy+2x+2y=2x^2+2y^2\)
⇔ \(\left(x^2+y^2-2xy\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)=2\)
⇔ \(\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2=2\)
⇔ 
⇔ 
Các cặp số nguyên (x, y) thỏa mãn phương trình là : (0; 0); (2; 2); (0; 1); (2; 1); (1; 0);(1;2).
Giải hệ phương trình: x + y 2 + y = 3 2 x 2 + y 2 + x y + x = 5 ta được số nghiệm là:
A. 4
B. 3
C. 2
D. 1
Ta có x + y 2 + y = 3 2 x 2 + y 2 + x y + x = 5 ⇔ 2 x 2 + 4 x y + 2 y 2 + 2 y = 6 2 x 2 + 2 y 2 + 2 x y + x = 5
Suy ra 2xy + 2y – x – 1 = 0 ⇔ (x + 1) (2y – 1) = 0 ⇔ x = −1 hoặc y = 1 2
Với x = −1, ta được y 2 – y – 2 = 0 ⇔ y = − 1 y = 2
Ta được hai nghiệm (−1; −1) và (−1; 2)
Với y = 1 2 , ta được x 2 + x − 9 4 = 0 ⇔ x = − 1 ± 10 2
Ta được hai nghiệm − 1 − 10 2 ; 1 2 và − 1 + 10 2 ; 1 2
Vậy hệ có bốn nghiệm (−1; −1); (−1; 2); − 1 − 10 2 ; 1 2 và − 1 + 10 2 ; 1 2
Đáp án:A
Giải hệ phương trình: x y − y 2 = 3 y − 1 − x + 2 y − 1 1 x 3 y − 4 x 2 + 7 x y − 5 x − y + 2 = 0 2
(với x ; y ) ta được nghiệm là (x; y). Khi đó x. y bằng:
A. 4
B. 3
C. 2
D. 1
ĐK: y ≥ 1 3 x + 2 y ≥ 1 ⇔ x ≥ 1 − 2 y y ≥ 1 3
Xét 3 y − 1 + x + 2 y − 1 = 0 ⇔ x = y = 1 3
Thay vào (2) không thỏa mãn
Xét 3 y − 1 + x + 2 y − 1 ≠ 0 ⇔ x ≠ 1 3 y ≠ 1 3
(1) ⇔ y ( x – y ) = y − x 3 y − 1 + x + 2 y − 1
Với x = y, thay vào (2) ta được:
x 4 – 4 x 3 + 7 x 2 − 6 x + 2 = 0 ⇔ ( x – 1 ) 2 ( x 2 – 2 x + 2 ) = 0 ⇔ x = 1
Khi đó: y = 1 (TM). Vậy nghiệm của hệ là (1; 1)
Nên x. y = 1
Đáp án:B
Giải phương trình nghiệm nguyên 7(x+y)=3(x2−xy+y2)
Giúp mình với các bạn!
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình x y + y 2 + x = 7 y ( 1 ) x 2 y + x = 12 ( 2 ) thì tích xy bằng:
A. 1
B. 2
C. 3
D. 4
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

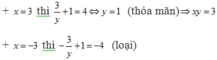

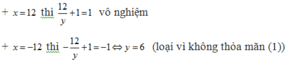
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
Hệ phương trình x 2 + y 2 = 4 x + y = 2 có nghiệm là (x; y) với x > y. Khi đó xy bằng:
A. 0
B. 1
C. 2
D. 4
Hệ phương trình x 2 + y 2 = 4 x + y = 2 có nghiệm là (x; y) với x > y. Khi đó tích xy bằng:
A. 0
B. 1
C. 2
D. 4
Đáp án A
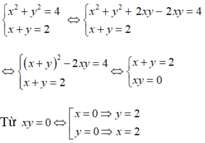
Vậy hệ phương trình có hai nghiệm (x; y) = (0; 2); (x; y) = (2; 0) Từ giả thiết x > y nên x = 2; y = 0 ⇒ xy = 0
Tập nghiệm của hệ phương trình x + y + x y = - 13 x 2 + y 2 - x - y = 32 là:
A. - 5 ; 2 ; 5 ; - 3
B. - 5 ; 2 ; 5 ; - 3 ; - 3 ; 5
C. - 5 ; 2 ; - 2 ; 5 ; 5 ; - 3 ; - 3 ; 5
D. - 5 ; 2 ; 2 ; - 5 ; 5 ; - 3 ; - 3 ; 5
t 2
Ta có: x + y + x y = - 13 x 2 + y 2 - x - y = 32 ⇔ x + y + x y = - 13 ( x + y ) 2 - 2 x y - ( x + y ) = 32
Đặt S = x+ y; P = xy . Khi đó, hệ phương trình trên trở thành:
S + P = - 13 ( 1 ) S 2 - 2 P - S = 32 ( 2 )
Từ (1) suy ra: P = -S – 13 thay vào (2) ta được:
S 2 – 2(-S – 13) – S = 32
⇔ S 2 + 2 S + 26 - S - 32 = 0 ⇔ S 2 + S - 6 = 0 ⇔ [ S = 2 S = - 3
* Với S = 2 thì P = -15 . Khi đó , x và y là nghiệm phương trình:
t 2 - 2t – 15 = 0 ⇔ [ t = 5 t = - 3
* Với S = -3 thì P = -10. Khi đó, x và y là nghiệm phương trình:
t 2 + 3t – 10 =0 ⇔ [ t = 2 t = - 5
Vậy hệ phương trình đã cho có 4 nghiệm ( 5; -3); (-3; 5); (2; -5); (-5; 2).
Chọn D.