1.√x2−2x+5=x2−2x−1

Những câu hỏi liên quan
tìm x:
a)3(2x-3)+2(2-x)=-3
b)2x(x2-2)+x2(1-2x)-x2=-12
c)3x(2x+3)-(2x+5)(3x-2)=8
d)4x(x - 1) - 3(x2-5)-x2=(x-3)-(x+4)
e)2(3x-1)(2x+5)-6(2x-1)(x+2)=-6
a: Ta có: \(3\left(2x-3\right)+2\left(2-x\right)=-3\)
\(\Leftrightarrow6x-9+4-2x=-3\)
\(\Leftrightarrow4x=2\)
hay \(x=\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
Bài 1: Thu gọn các biểu thức saua)(2x2 + 5x - 2)(2x2 - 4x +3)b)(2x -3)(3x - 2) - 3x(2x - 5)c)(x -1)(x2 + x + 1) - (x + 1)(x2 - x +1)d)(x2 + x - 1)(x2 - x + 1)e)(2 + 3y)2 - (2x -3y)2 -12xyd)(x2 - 4x)(5 + 2x - x2)cảm ơn!giúp mình với chiều nay ktra 15ph T_T
Đọc tiếp
Bài 1: Thu gọn các biểu thức sau
a)(2x2 + 5x - 2)(2x2 - 4x +3)
b)(2x -3)(3x - 2) - 3x(2x - 5)
c)(x -1)(x2 + x + 1) - (x + 1)(x2 - x +1)
d)(x2 + x - 1)(x2 - x + 1)
e)(2 + 3y)2 - (2x -3y)2 -12xy
d)(x2 - 4x)(5 + 2x - x2)
cảm ơn!giúp mình với chiều nay ktra 15ph T_T
thu gọn biểu thức
a) (6x-2)2+4(3x-1)(2+y)+(y+2)2-(6x+y)2
b)5(2x-1)2+2(x-1)(x+3)-2(5-2x)2-2x(7x+12)
c)2(5x-1)(x2-5x+1)+(x2-5x+1)2+(5x-1)2-(x2-1)(x2+1)
d)(x2+4)2-(x2+4)(x2-4)(x2+16)-8(x-4)(x+4)
`#3107`
`a)`
`(6x - 2)^2 + 4(3x - 1)(2 + y) + (y + 2)^2 - (6x + y)^2`
`= [(6x - 2)^2 - (6x + y)^2] + 4(3x - 1)(2 + y) + (2 + y)^2`
`= (6x - 2 - 6x - y)(6x -2 + 6x + y) + (2 + y)*[ 4(3x - 1) + 2 + y]`
`= (2 - y)(12x + y - 2) + (2 + y)*(12x - 4 + 2 + y)`
`= (2 - y)(12x + y - 2) + (2 + y)*(12x + y - 2)`
`= (12x + y - 2)(2 - y + 2 + y)`
`= (12x + y - 2)*4`
`= 48x + 4y - 8`
`b)`
\(5(2x-1)^2+2(x-1)(x+3)-2(5-2x)^2-2x(7x+12)\)
`= 5(4x^2 - 4x + 1) + 2(x^2 + 2x - 3) - 2(25 - 20x + 4x^2) - 14x^2 - 24x`
`= 20x^2 - 20x + 5 + 2x^2 + 4x - 6 - 50 + 40x - 8x^2 - 14x^2 - 24x`
`= - 51`
Đúng 4
Bình luận (0)
`c)`
\(2(5x-1)(x^2-5x+1)+(x^2-5x+1)^2+(5x-1)^2-(x^2-1)(x^2+1)\)
`= [ 2(5x - 1) + x^2 - 5x + 1] * (x^2 - 5x + 1) + (5x - 1)^2 - [ (x^2)^2 - 1]`
`= (10x - 2 + x^2 - 5x + 1) * (x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`
`= (x^2 + 5x - 1)(x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`
`= x^4 - (5x - 1)^2 + (5x - 1)^2 - x^4 + 1`
`= 1`
`d)`
\((x^2+4)^2-(x^2+4)(x^2-4)(x^2+16)-8(x-4)(x+4)\)
`= (x^2 + 4)*[x^2 + 4 - (x^2 - 4)(x^2 + 16)] - 8(x^2 - 16)`
`= (x^2 + 4)(x^4 + 12x^2 - 64) - 8x^2 + 128`
`= x^6 + 16x^4 - 16x^2 - 256 - 8x^2 + 128`
`= x^6 + 16x^4 - 24x^2 - 128`
Đúng 2
Bình luận (0)
Hàm số bậc hai
y
a
x
2
-
2
x
+
c
có đồ thị với đỉnh I(2; -1) là A. y (
x
2
/ 2) - 2x + 1 B. y (
x
2
/ 2) - 2x + 3 C. y
x
2
- 2x - 1 D. y 2
x...
Đọc tiếp
Hàm số bậc hai y = a x 2 - 2 x + c có đồ thị với đỉnh I(2; -1) là
A. y = ( x 2 / 2) - 2x + 1
B. y = ( x 2 / 2) - 2x + 3
C. y = x 2 - 2x - 1
D. y = 2 x 2 - 2x - 5
Đáp án: A (kiểm tra hoành độ đỉnh x = (-b)/2a; sai đó kiểm tra tung độ đỉnh)
Đúng 0
Bình luận (0)
Mọi người làm nhanh hộ e với ạ, T7 e nộp rBài 1.Tính:a. x2(x–2x3) b. (x2+ 1)(5–x) c. (x–2)(x2+ 3x–4) d. (x–2)(x–x2+ 4)e. (x2–1)(x2+ 2x) f. (2x–1)(3x + 2)(3–x) g. (x + 3)(x2+ 3x–5)h (xy–2).(x3–2x–6) i. (5x3–x2+ 2x–3).(4x2–x + 2)Bài 2.Tính:a. (x–2y)2 b. (2x2+3)2 c. (x–2)(x2+ 2x + 4) d. (2x–1)2Bài 3: Rút gọn biểu thứca.(6x + 1)2+ (6x–1)2–2(1 + 6x)(6x–1)b. x(2x2–3)–x2(5x + 1) + x2.c. 3x(x–2)–5x(1–x)–8(x2–3)Bài 4: Tìm x, biếta. (x–2)2–(x–3)(x + 3) 6.b. 4(x–3)2–(2x–1)(2x + 1) 10c. (x–4...
Đọc tiếp
Mọi người làm nhanh hộ e với ạ, T7 e nộp r![]()
Bài 1.
Tính:
a. x2(x–2x3) b. (x2+ 1)(5–x) c. (x–2)(x2+ 3x–4) d. (x–2)(x–x2+ 4)
e. (x2–1)(x2+ 2x) f. (2x–1)(3x + 2)(3–x) g. (x + 3)(x2+ 3x–5)
h (xy–2).(x3–2x–6) i. (5x3–x2+ 2x–3).(4x2–x + 2)
Bài 2.
Tính:
a. (x–2y)2 b. (2x2+3)2 c. (x–2)(x2+ 2x + 4) d. (2x–1)2
Bài 3: Rút gọn biểu thức
a.(6x + 1)2+ (6x–1)2–2(1 + 6x)(6x–1)
b. x(2x2–3)–x2(5x + 1) + x2.
c. 3x(x–2)–5x(1–x)–8(x2–3)
Bài 4: Tìm x, biết
a. (x–2)2–(x–3)(x + 3) = 6.
b. 4(x–3)2–(2x–1)(2x + 1) = 10
c. (x–4)2–(x–2)(x + 2) = 6.
d. 9 (x + 1)2–(3x–2)(3x + 2) = 10
Bài 5:Phân tích các đa thức sau thành nhân tử
a. 1–2y + y2
b. (x + 1)2–25
c. 1–4x2
d. 8–27x3
e. 27 + 27x + 9x2+ x3
f. 8x3–12x2y +6xy2–y3
g. x3+ 8y3
Bài 6:Phân tích các đa thức sau thành nhân tử
a. 3x2–6x + 9x2
b. 10x(x–y)–6y(y–x)
c. 3x2+ 5y–3xy–5x
d. 3y2–3z2+ 3x2+ 6xy
e. 16x3+ 54y3
f. x2–25–2xy + y2
g. x5–3x4+ 3x3–x2
.
Bài 7: Phân tích đa thức thành nhân tử
a. 5x2–10xy + 5y2–20z2
b. 16x–5x2–3
c. x2–5x + 5y–y2
d. 3x2–6xy + 3y2–12z2
e. x2+ 4x + 3
f. (x2+ 1)2–4x2
g. x2–4x–5
Bài 5:
a. 1 - 2y + y2
= (1 - y)2
b. (x + 1)2 - 25
= (x + 1)2 - 52
= (x + 1 - 5)(x + 1 + 5)
= (x - 4)(x + 6)
c. 1 - 4x2
= 12 - (2x)2
= (1 - 2x)(1 + 2x)
d. 8 - 27x3
= 23 - (3x)3
= (2 - 3x)(4 + 6x + 9x2)
e. (đề hơi khó hiểu ''x3'' !?)
g. x3 + 8y3
= (x + 2y)(x2 - 2xy + y2)
Đúng 1
Bình luận (0)
Bài 2: Tínha) ( x4 - x3 + x2 + 3x ) : ( x2 - 2x + 3 )b) ( 21x2y3 ) : ( 6xy) c) x2- 36 : ( 2x + 10) ( 6 - x )d) 2x2 ( 3x - 5 )e) ( 12x3y + 18x2y) : 2xyg) ( x2 + 2x + 1 ) : ( x + 1 )h) 5y ( 2y - 1 ) - ( 3y + 2 ) ( 3 - 3y)i) ( 6x3 - x2 + 5x - 1 ) : ( 2x - 1 )
Đọc tiếp
Bài 2: Tính
a) ( x4 - x3 + x2 + 3x ) : ( x2 - 2x + 3 )
b) ( 21x2y3 ) : ( 6xy)
c) x2- 36 : ( 2x + 10) ( 6 - x )
d) 2x2 ( 3x - 5 )
e) ( 12x3y + 18x2y) : 2xy
g) ( x2 + 2x + 1 ) : ( x + 1 )
h) 5y ( 2y - 1 ) - ( 3y + 2 ) ( 3 - 3y)
i) ( 6x3 - x2 + 5x - 1 ) : ( 2x - 1 )
`@` `\text {Ans}`
`\downarrow`

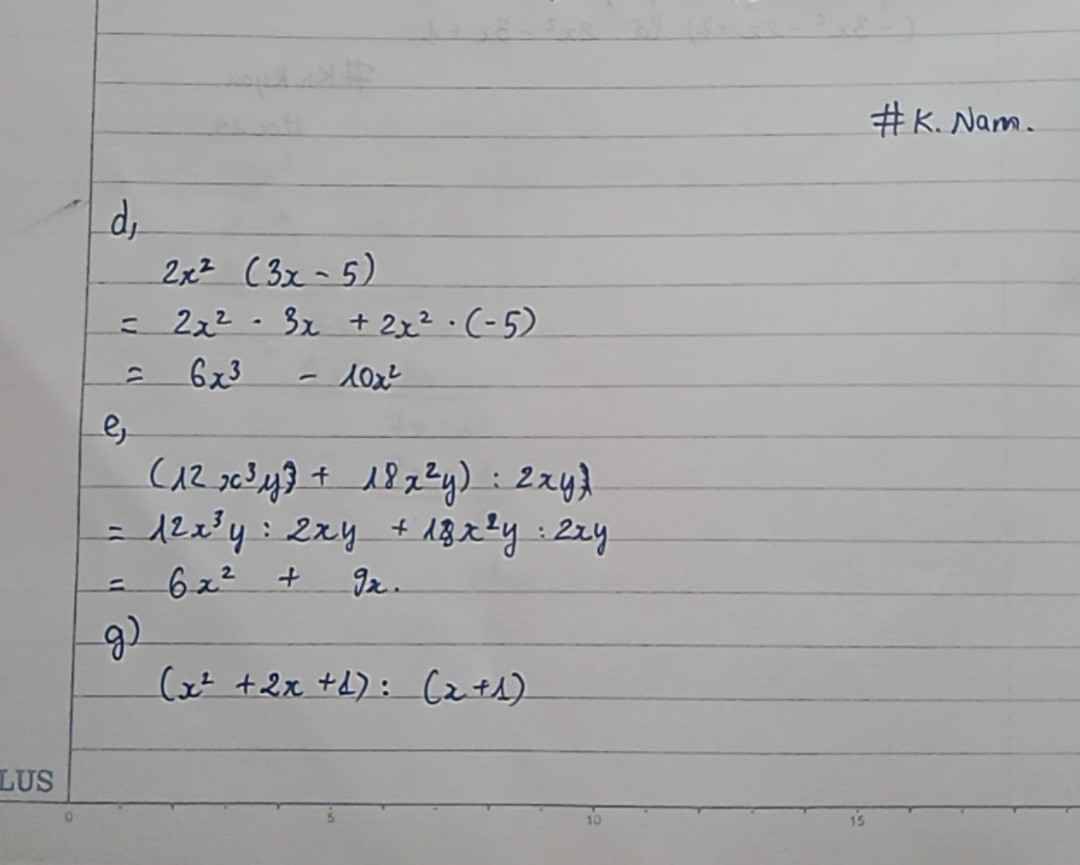

*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.
Đúng 5
Bình luận (0)
Giải phương trình
1
x
-
1
+
x
2
-
2
x
+
5
+
1
x
-
1
-
x
2...
Đọc tiếp
Giải phương trình 1 x - 1 + x 2 - 2 x + 5 + 1 x - 1 - x 2 - 2 x + 5 = 1
A. x = −2
B. x = 0
C. x = 1
D. x = −1
1Giải các phương trình sau bằng cách đưa về phương trình tích:
a) 3x(2x – 3) = 5(3 – 2x)
b) (x2 + 1)(2x + 5) = (x – 1)(x2 + 1)
c) 3x3 = x2 + 3x - 1
d) x2 – 9x + 20 = 0
2Giải các phương trình sau bằng cách đưa về phương trình tích:
a) 3x(2x – 3) = 5(3 – 2x)
b) (x2 + 1)(2x + 5) = (x – 1)(x2 + 1)
c) 3x3 = x2 + 3x - 1
d) x2 – 9x + 20 = 0
a/ \(3x(2x-3)=5(3-2x) \Leftrightarrow 3x(2x-3)+5(2x-3)=0 \\\ \Leftrightarrow (2x-3)(3x+5)=0 \)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{3}{2}\\x=-\frac{5}{3}\end{matrix}\right.\)
KL: .............
b/ \(\left(x^2+1\right)\left(2x+5\right)=\left(x-1\right)\left(x^2+1\right)\Leftrightarrow\left(x^2+1\right)\left(2x+5\right)-\left(x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(2x+5-x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x+6=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=-6\end{matrix}\right.\)
KL: .............
c/ \(3x^3=x^2+3x-1\Leftrightarrow3x^3-x^2-3x+1=0\Leftrightarrow x^2\left(3x-1\right)-\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-1\right)=0\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{3}\\x=1\\x=-1\end{matrix}\right.\)
KL: ..........
d/ \(x^2-9x+20=0\Leftrightarrow x^2-5x-4x+20=0\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\end{matrix}\right.\)
KL: .............
Đúng 0
Bình luận (0)
\(a,3x\left(2x-3\right)=5\left(3-2x\right)\Leftrightarrow6x^2-9x=15-10x\Leftrightarrow6x^2-9x-15+10x=0\Leftrightarrow6x^2+x-15=0\Leftrightarrow\left(3x+5\right)\left(2x-3\right)=0\)
\(\left(3x+5\right)\left(2x-3\right)=0\)
\(\left[{}\begin{matrix}x=-\frac{5}{3}\\x=\frac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x biết:
a) (x+5).(2x+1)=0
b) x.(x+2)-3.(x+2)=0
c) 2x.(x-5)-x.(3+2x)=26
d) x2-10x-8x+16=0
e) x2-10x=25
f) 5x.(x-1)=x-1
g) 2.(x+5)-x2-5x=0
h) x2+5x-6=0
i) (2x-3)2-4.(x+1).(x-1)=49
j) x3+x2+x+1=0
k) x3-x2=4x2-8x+4
Mn ơi giúp em vs ạ,em cảm ơn trc ạ
\(a,\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{2}\end{matrix}\right.\\ b,\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\\ c,\Leftrightarrow2x^2-10x-3x-2x^2=26\\ \Leftrightarrow-13x=26\Leftrightarrow x=-2\\ d,\Leftrightarrow x^2-18x+16=0\\ \Leftrightarrow\left(x^2-18x+81\right)-65=0\\ \Leftrightarrow\left(x-9\right)^2-65=0\\ \Leftrightarrow\left(x-9+\sqrt{65}\right)\left(x-9-\sqrt{65}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=9-\sqrt{65}\\9+\sqrt{65}\end{matrix}\right.\)
\(e,\Leftrightarrow x^2-10x-25=0\\ \Leftrightarrow\left(x-5\right)^2-50=0\\ \Leftrightarrow\left(x-5-5\sqrt{2}\right)\left(x-5+5\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5+5\sqrt{2}\\x=5-5\sqrt{2}\end{matrix}\right.\\ f,\Leftrightarrow5x\left(x-1\right)-\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(5x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\\ g,\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ h,\Leftrightarrow x^2+2x+3x+6=0\\ \Leftrightarrow\left(x+3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\\ i,\Leftrightarrow4x^2-12x+9-4x^2+4=49\\ \Leftrightarrow-12x=36\Leftrightarrow x=-3\)
\(j,\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\Leftrightarrow x=-1\\ k,\Leftrightarrow x^2\left(x-1\right)=4\left(x-1\right)^2\\ \Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải pt : a) 2/-x2+6x-8 - x-1/x-2 = x+3/x-4
b) 2/x3-x2-x+1 = 3/1-x2 - 1/x+1
c) x+2/x-2 - 2/x2-2x = 1/x
d) 5/-x2+5x-6 + x+3/2-x = 0
e) x/2x+2 - 2x/x2-2x-3 = x/6-2x
f) 1/x-1 - 3x2/x3-1 = 2x/x2+x-1























