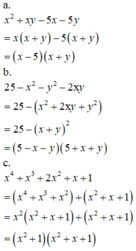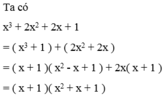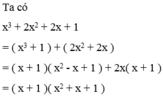Phân tích các đa thức sau thành nhân tử: x3 - 2x2 +5x

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tửa)
x
2
+
x
y
−
5
x
−
5
y
b)
25
−
x
2
−
y
2
−
2
x
y
c)
x
4
+
x
3
+
2
x
2
+...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử
a) x 2 + x y − 5 x − 5 y
b) 25 − x 2 − y 2 − 2 x y
c) x 4 + x 3 + 2 x 2 + x + 1
Phân tích các đa thức sau thành nhân tử x 3 + 2 x 2 + 2 x + 1
Phân tích đa thức sau thành nhân tử: x3 – 2x2 + x.
x3 – 2x2 + x
= x.x2 – x.2x + x (Xuất hiện nhân tử chung là x)
= x(x2 – 2x + 1) (Xuất hiện hằng đẳng thức (2))
= x(x – 1)2
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử : x3+ 2x2 +x
\(x^3+2x^2+x\)
\(=x\left(x^2+2x+1\right)\)
\(=x\left(x+1\right)^2\)
Đúng 1
Bình luận (0)
\(x\left(x^2+2x+1\right)=x\left(x+1\right)^2\)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử x 3 + 2 x 2 + 2 x + 1 ( a b - 1 ) 2 + ( a + b ) 2
x3 + 2x2 - 2x -1 → phân tích đa thức sau thành nhân tử ?
= x^3 - x^2 + 3x^2 - 3x + x - 1
= (x - 1)(x^2 + 3x + 1)
Đúng 4
Bình luận (0)
\(x^3+2x^2-2x-1\)
\(=\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+3x+1\right)\)
Đúng 4
Bình luận (0)
Phân tích đa thức sau thành nhân tử: x3 – 2x2 + x – xy2
x3 – 2x2 + x – xy2
(Có nhân tử chung x)
= x(x2 – 2x + 1 – y2)
(Có x2 – 2x + 1 là hằng đẳng thức).
= x[(x – 1)2 – y2]
(Xuất hiện hằng đẳng thức (3))
= x(x – 1 + y)(x – 1 – y)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
b ) x 3 – x 2 – 5 x + 125
b) x3 – x2 – 5x + 125
= (x3 + 125) - (x2 + 5x)
= (x + 5)(x2 - 5x + 25) - x(x + 5)
= (x + 5)(x2 - 5x + 25 - x)
= (x + 5)(x2 - 6x + 25)
Đúng 0
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử
a) x3-2x2-5x+6
b) x4+5x2+6
c) x3+4x2+5x+2
d) x4+324
phân tích các đa thức thành nhân tử
a) x2-2xy +y2-z2
b) x3+y3+2x2-2xy+2y2
\(a,x^2-2xy+y^2-z^2=\left(x-y\right)^2-z^2=\left(x-y-z\right).\left(x-y+z\right)\)
\(b,x^3+y^3+2x^2-2xy+2y^2=\left(x^3+y^3\right)+2\left(x^2-xy+y^2\right)=\left(x+y\right).\left(x^2-2xy+y^2\right)+2.\left(x^2-xy+y^2\right)=\left(x^2-xy+y^2\right).\left(x+y+2\right)\)
Đúng 3
Bình luận (0)