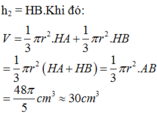Cho tam giác OAB vuông cân tại O, cạnh OA=4cm. Tính |2 vecto OA - vecto OB|

Những câu hỏi liên quan
Cho tam giác OAB vuông cân tại O với OA=OB=a. Độ dài của vecto u=12/4 OA - 5/2 OB
Cho tam giác OAB vuông cân tại O, cạnh OA a. Tính
2
O
A
→
−
O
B
→
.
A. a B.
1
+
2
a
.
C.
a
5
.
D.
2
a...
Đọc tiếp
Cho tam giác OAB vuông cân tại O, cạnh OA= a. Tính 2 O A → − O B → .
A. a
B. 1 + 2 a .
C. a 5 .
D. 2 a 2 .
Cho tam giác OAB vuông cân tại O, cạnh OA a = . Tính 2OA-OB
tam giác OAB vuông cân tại O \(\Rightarrow\)OA = OB = a.
2OA - OB = 2OA - OA = OA =a
Đúng 0
Bình luận (0)
\(2\cdot OA-OB=2\cdot OA-OA=OA=a\)
Đúng 0
Bình luận (0)
cho tam giác OAB .giả sử
{vecto OA + vecto OB = vecto OM
{vecto OA -vecto OB= vecto ON
a, khi nào thì điểm M nằm trên đường phân giác trọng của góc AOB?
b, ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,ngoài,,,,,,,,,,,,,,,,,,,,,,,,,,?
mình sửa lại ý
b, khi nào thì N nằm trên đường phân giác ngoài của góc AOB
Đúng 0
Bình luận (0)
Cho hình vuông ABCD, cạnh 8cm. Tính độ dài các vecto sau:
a) vecto OA + vecto OB
b) vecto OA - vecto OB
c) 3 vecto OA - 2 vecto OB
d) 3/4 vecto OA + 5/2 vecto OB
a: Kẻ OH\(\perp\)AB
OH\(\perp\)AB
AD\(\perp\)AB
Do đó OH//AD
Xét ΔBAD có
O là trung điểm của BD
OH//AD
Do đó: H là trung điểm của AB
=>\(OH=\dfrac{AD}{2}=\dfrac{8}{2}=4\)
XétΔOAB có OH là trung tuyến
nên \(\overrightarrow{OA}+\overrightarrow{OB}=2\cdot\overrightarrow{OH}\)
=>\(\left|\overrightarrow{OA}+\overrightarrow{OB}\right|=2\cdot OH=2\cdot4=8\)
b: \(\left|\overrightarrow{OA}-\overrightarrow{OB}\right|=\left|\overrightarrow{BO}+\overrightarrow{OA}\right|=\left|\overrightarrow{BA}\right|\)
\(=BA=8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OA=OB=OC = x Gọi H là trực tâm tam giác ABC. M,N lần lượt là trung điểm OB,BC. G là trọng tâm tam giác OBC. P thuộc cạnh AC sao cho PA = 2PC Đặt OA= vecto a, OB= vecto b, OC= vecto c a). Hãy biểu diễn các vecto MG, PN theo a, b, c b) Tính góc giữa hai đường thàng MP và CN. c) Chứng minh rằng OH vuông góc HB
Cho tam giác OAB vuông tại O, OA 3cm, OB 4cm. Quay tam giác OAB quanh cạnh AB. Thể tích khối tròn xoay được tạo thành gần nhất giá trị nào? A. 28
c
m
3
B. 26
c
m
3
C. 32
c
m
3
D. 30
c
m
3
Đọc tiếp
Cho tam giác OAB vuông tại O, OA = 3cm, OB = 4cm. Quay tam giác OAB quanh cạnh AB. Thể tích khối tròn xoay được tạo thành gần nhất giá trị nào?
A. 28 c m 3
B. 26 c m 3
C. 32 c m 3
D. 30 c m 3
cho tam giac OAB vuông cân tại A, cạnh OA= a. Tính |3vecto OA + 4vecto OB| theo a
Lời giải:
\(A=|3\overrightarrow{OA}+4\overrightarrow{OB}|\\ \Rightarrow A^2=9OA^2+16OB^2+24\overrightarrow{OA}.\overrightarrow{OB}\)
\(A^2=9a^2+16.2a^2+\overrightarrow{OA}(\overrightarrow{OA}+\overrightarrow{AB})=41a^2+OA^2+\overrightarrow{OA}.\overrightarrow{AB}\\ =41a^2+a^2+0=42a^2\)
(do $OA, AB$ vuông góc với nhau)
$\Rightarrow A=\sqrt{42}a$
Đúng 1
Bình luận (0)
cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau tại O và OA=OB=OC=1. Gọi M là trung điểm AB. tính (vecto OM,vecto BC)