Ta có:

\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB=10.0,8=8\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\)

b.

\(sinC=\dfrac{AB}{BC}=\dfrac{8}{10}=0,8\)

\(cosC=\dfrac{AC}{BC}=\dfrac{6}{10}=0,6\)

\(tanC=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)

\(cotC=\dfrac{AC}{AB}=\dfrac{3}{4}\)

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

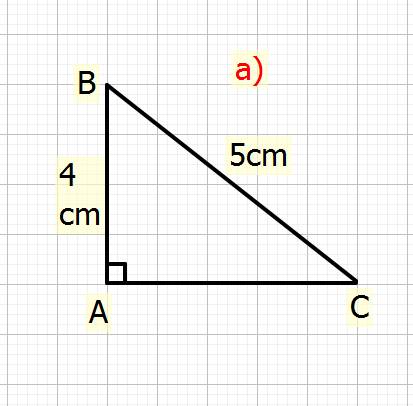
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

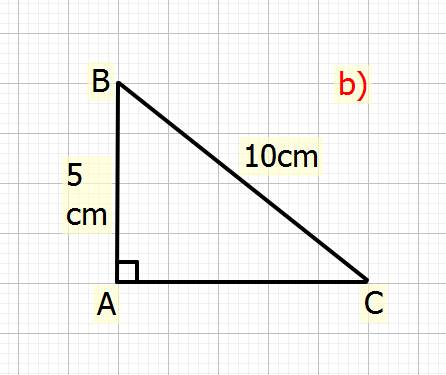
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

AA lai Aa

Theo đề ta tính được :

tan B= AC/AB=4/3 

cot B= AB/AC=3/4

TAN c= AB/AC=3/4

COT C= AC/AB = 4/3 

Dựa trên bài tập 14 trong sách giáo khoa ta có:

tan B= sinB/ cos B = 4/3 thay số vào ta tính đc sin B và cos B

tan C = sin C/ cos C = 3/4 thay số vào tính ta được sin C và cos C

=> tính đc tỷ số lượng giác.

(_ Mk chỉ bày cách tính hoy cậu tự làm để nhớ nhé !!_)

Câu 1:

a: ΔAHB vuông tại H

=>\(AB^2=AH^2+HB^2\)

=>\(BH^2=30^2-24^2=\left(30-24\right)\left(30+24\right)=6\cdot54=6\cdot6\cdot9=6^2\cdot3^2=18^2\)

=>BH=18(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(BH\cdot BC=BA^2\)

=>\(18\cdot BC=30^2=900\)

=>\(BC=\frac{900}{18}=50\left(\operatorname{cm}\right)\)

b: Xét ΔHAB vuông tại H có \(\sin HAB=cosB=\frac{HB}{AB}=\frac{18}{30}=\frac35\)
\(cosHAB=\sin B=\frac{AH}{AB}=\frac{24}{30}=\frac45\)

tan HAB=cot B\(=\frac{HB}{AH}=\frac{18}{24}=\frac34\)

cot HAB=tan B\(=\frac{AH}{HB}=\frac{24}{18}=\frac43\)

Bài 2:

a: BH+HC=BC

=>BC=4+9=13(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(BH\cdot BC=BA^2\)

=>\(BA^2=4\cdot13=52\)

=>\(BA=\sqrt{52}=2\sqrt{13}\left(\operatorname{cm}\right)\)

ΔCAB vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=169-52=117\)

=>\(AC=3\sqrt{13}\left(\operatorname{cm}\right)\)

b: Xét ΔABC vuông tại A có sin C\(=\frac{AB}{BC}=\frac{2\sqrt{13}}{13}\)

nên \(\hat{C}\) ≃34 độ

ΔABC vuông tại A

=>\(\hat{B}+\hat{C}=90^0\)

=>\(\hat{B}=90^0-34^0=56^0\)

Xét ΔABC vuông tại A ta có:

cos\(\widehat{ABC}\) = sin\(\widehat{ACB}\)

=>sin\(\widehat{ACB}\)=1/3