giải và biện luận các phương trình sau:
a) m2x+2m=9x+m-3
b) m2x+2=-4x
c) 2m2x-3=3mx-x+m-4
Giải và biện luận các phương trình sau theo tham số m
2 m x - 2 + 4 = 3 - m 2 x
Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm ![]()
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.
Giải và biện luận các phương trình sau
a) 4x-2=m(mx-1)
f) m2x-3=4x-(m-1)
g)m3x-4=m2+4mx-4m
Giải và biện luận các phương trình sau
a) 4x-2=m(mx-1)
f) m2x-3=4x-(m-1)
g)m3x-4=m2+4mx-4m
a: \(4x-2=m\left(mx-1\right)\)(1)
=>\(m^2x-m=4x-2\)
=>\(x\left(m^2-4\right)=m-2\)
=>x(m-2)(m+2)=m-2
TH1: m=2
Phương trình (1) sẽ trở thành \(x\left(2-2\right)\left(2+2\right)=2-2\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (1) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-2-2\)
=>0x=-4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (1) sẽ trở thành: \(x\left(m-2\right)\left(m+2\right)=m-2\)
=>x(m+2)=1
=>\(x=\dfrac{1}{m+2}\)
f: \(m^2x-3=4x-\left(m-1\right)\)(2)
=>\(m^2x-4x=-m+1+3\)
=>\(x\left(m^2-4\right)=-m+2\)
=>\(x\left(m-2\right)\left(m+2\right)=-\left(m-2\right)\)
TH1: m=2
Phương trình (2) sẽ trở thành: \(x\left(2-2\right)\left(2+2\right)=-\left(2-2\right)\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (2) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-\left(-2-2\right)\)
=>0x=4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (2) sẽ là: x(m-2)(m+2)=-(m-2)
=>x(m+2)=-1
=>\(x=-\dfrac{1}{m+2}\)
g: \(m^3x-4=m^2+4mx-4m\)(3)
=>\(m^3x-4mx=m^2-4m+4\)
=>\(x\left(m^3-4m\right)=\left(m-2\right)^2\)
=>\(x\cdot m\cdot\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
TH1: m=2
Phương trình (3) sẽ trở thành: \(x\cdot2\cdot\left(2+2\right)\left(2-2\right)=\left(2-2\right)^2\)
=>0x=0(luôn đúng)
TH2: m=0
Phương trình (3) sẽ trở thành:
\(x\cdot0\cdot\left(0+2\right)\left(0-2\right)=\left(0-2\right)^2\)
=>0x=4
=>\(x\in\varnothing\)
TH3: m=-2
Phương trình (3) sẽ trở thành;
\(x\cdot\left(-2\right)\left(-2+2\right)\left(-2-2\right)=\left(-2-2\right)^2\)
=>0x=16
=>\(x\in\varnothing\)
TH4: \(m\notin\left\{0;2;-2\right\}\)
Phương trình (3) sẽ trở thành:
\(x\cdot m\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
=>\(x=\dfrac{\left(m-2\right)^2}{m\left(m+2\right)\left(m-2\right)}=\dfrac{m-2}{m\left(m+2\right)}\)
Giải và biện luận các phương trình sau theo tham số m: m2x + 6 = 4x + 3m
m2x + 6 = 4x + 3m
⇔ m2.x – 4x = 3m – 6
⇔ (m2 – 4).x = 3m – 6 (2)
+ Xét m2 – 4 ≠ 0 ⇔ m ≠ ±2, phương trình (2) có nghiệm duy nhất:
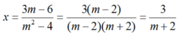
+ Xét m2 – 4 = 0 ⇔ m = ±2
● Với m = 2, pt (2) ⇔ 0x = 0 , phương trình có vô số nghiệm
● Với m = –2, pt (2) ⇔ 0x = –12, phương trình vô nghiệm.
Kết luận:
+ m = 2, phương trình có vô số nghiệm
+ m = –2, phương trình vô nghiệm
+ m ≠ ±2, phương trình có nghiệm duy nhất 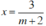
Giải và biện luận các phương trình sau theo tham số m
a) m(x - 2) = 3x + 1;
b) m2x + 6 = 4x + 3m;
c) (2m + 1)x – 2m = 3x – 2.
a) ⇔ (m – 3)x = 2m + 1.
Nếu m ≠ 3 phương trình có nghiệm duy nhất x = .
Nếu m = 3 phương trình trở thành 0x = 7. Vô nghiệm.
b) ⇔ (m2 – 4)x = 3m – 6.
Nếu m2 – 4 ≠ 0 ⇔ m ≠ ± 2, có nghiệm x = .
Nếu m = 2, phương trình trở thành 0x = 0, mọi x ∈ R đều nghiệm đúng phương trình.
Nếu m = -2, phương trình trở thành 0x = -12. Vô nghiệm.
c) ⇔ 2(m – 1)x = 2(m-1).
Nếu m ≠ 1 có nghiệm duy nhất x = 1.
Cho các phương trình có tham số m sau:
3 m x - 1 = m x + 2 (1); m x + 2 = 2 m x + 1 (2);
m m x - 1 = m 2 x + 1 - m (3); m x - m + 2 = 0 (4).
Phương trình luôn vô nghiệm với mọi giá trị của m là:
A. Phương trình (1)
B. Phương trình (2)
C. Phương trình (3)
D. Phương trình (4).
Phương trình ax + b = 0 hoặc ax = b vô nghiệm khi a= 0 và b ≠ 0 .
Xét phương án C:
m m x - 1 = m 2 + 1 x - m ⇔ m 2 x = m 2 x + 1 - m
⇔ 0 x = 1 (vô lí) nên phương trình này vô nghiệm.
Chọn C.
m2x-m = 9x-3 tìm m để phương trình vô nghiệm
\(PT\Leftrightarrow x\left(m^2-9\right)-\left(m-3\right)=0\)
PT vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}m^2-9=0\\m-3\ne0\end{matrix}\right.\Leftrightarrow m=-3\)
\(\Leftrightarrow\left(m^2-9\right)x=m-3\)
Pt đã cho vô nghiệm khi:
\(\left\{{}\begin{matrix}m^2-9=0\\m-3\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=\pm3\\m\ne3\end{matrix}\right.\)
\(\Rightarrow m=-3\)
Cho các phương trình có tham số m sau:
m x + m = 0 (1); m - 2 x + 2 m = 0 (2);
m 2 + 1 x + 2 = 0 (3) ; m 2 x + 3 m + 2 = 0 (4).
Phương trình luôn có nghiệm duy nhất với mọi giá trị của m là:
A. Phương trình (1)
B. Phương trình (2)
C. Phương trình (3)
D. Phương trình (4)
Phương trình ax + b = 0 có nghiệm duy nhất khi a ≠ 0 .
Xét phương trình m 2 + 1 x + 2 = 0 có hệ số a= m2 + 1> 0 với mọi m.
Do đó, phương trình này luôn có nghiệm duy nhất với mọi giá trị của m.
Giải và biện luận các phương trình sau (với m là tham số):
a) mx – x – m + 2 = 0
\(b) m^2x + 3mx – m^2 + 9 = 0 \)
\(c) m^3x – m^2 - 4 = 4m(x – 1)\)
2) Cho phương trình ẩn x: . Hãy xác định các giá trị của k để phương trình trên có nghiệm x = 2.
\(mx-x-m+2=0\)
\(x\left(m-1\right)=m-2\)
Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)
Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)
Vậy ...