Cho hình vẽ như trên. Chứng minh MHMQ
Đọc tiếp
Cho hình vẽ như trên. Chứng minh MH<MQ
Những câu hỏi liên quan
Cho tam giác MNP vuông tại M, đường cao MH . a) Chứng minh DHNM đồng dạng với DMNP.b) Chứng minh hệ thức . Lấy điểm E tùy ý trên cạnh MP( E khác M; P) , vẽ điểm F trên cạnh MN sao cho , EF cắt MH tại điểm I. Chứng minh DNFH đồng dạng với DMEH và .
Đọc tiếp
Cho tam giác MNP vuông tại M, đường cao MH .
a) Chứng minh DHNM đồng dạng với DMNP.
b) Chứng minh hệ thức .
Lấy điểm E tùy ý trên cạnh MP( E khác M; P) , vẽ điểm F trên cạnh MN sao cho , EF cắt MH tại điểm I. Chứng minh DNFH đồng dạng với DMEH và .
Cho tam giác ABC vuông tại A .Có M là trung điểm BC . Vẽ MH vuông góc với AC .Trên tia HM lấy điểm K sao cho MK=MH ( Vẽ hình )Chứng minh: tam giác MHC= tam giác MKB và góc HKB=90oChứng minh: HK // AB ; KB=AHChứng minh: tam giác MAC cân
{ giúp tớ với tớ cảm mơn nhều với like cho ạ }♡♡
tu ke hinh :
a, xet tamgiac MHB va tamgiac MKC co : HM = MK (gt)
CM = MB do M la trung diem cua BC(gt)
goc HMB = goc KMC (doi dinh)
=> tamgiac MHB = tamgiac MKC (c - g - c)
xet tamgiac HMC va tamgiac KMB co : HM = MK (gt)
goc HMC = goc KMB (doi dinh)
MC = MB (cmt)
=> tamgiac HMC = tamgiac KMB (c - g - c)
=> goc CHM = goc MKB
ma goc CHM = 90 do MH | AC (gt)
=> goc MKB = 90
b, MH | AC (gt)
tamgiac ABC vuong tai A (gt) => AB | AC (dn)
2 duong thang nay phan biet
=> HK // AB (dl)
MH | AB (gt)
goc MKB = 90 (cau a) => MK | KB
2 duong thang nay phan biet
=> AC // KB (dl)
goc AHB so le trong HBK
=> goc AHB = goc HBK (tc)
xet tamgiac AHB va tamgiac KBH co : HB chung
goc HAB = 90 = goc HKB do. ...
=> tamgiac AHB = tamgiac KBH (ch - gn)
=> AH = KB (dn)
c, tamgiac HMC = tamgiac KMB (Cau a) => CH = KB
AH = KB (Cau b)
=> CH = HA
xet tamgiacHMC va tamgiac HMA co : HM chung
goc CHM = goc MHA do HM | AC (gt)
=> tamgiacHMC = tamgiac HMA (2cgv)
=> MC = MA (dn)
=> tamgiac MCA can tai M (dn)
Đúng 0
Bình luận (0)
a) xét tam giác MHC và tam giác HKB có
MK=MH (GT)
BM=MC(GT)
GÓC M1=GÓC M2 (đối đỉnh)
suy ra tam giác MHC bằng tam giác HKB (c-g-c)
do tam giác MHC bằng tam giác HKB nên góc H bằng góc K= 90 độ
suy ra góc HKB bằng 90độ
Đúng 0
Bình luận (0)
b) ta có
HM vuông góc AC
AB vuông góc AC
suy ra HK //AB
Nối M với A
Xét tam giác MHA và tam giác MKB
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ∆ABC vuông tại A, vẽ trung tuyến AM (M thuộc BC). Từ M kẻ MHvuông góc AC, trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a) Chứng minh ∆MHC = ∆MKB.
b) Chứng minh AB // MH.
a) Xét ΔMHC và ΔMKB có
MH=MK(gt)
\(\widehat{CMH}=\widehat{BMK}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔMHC=ΔMKB(c-g-c)
b) Ta có: HM⊥AC(gt)
AB⊥AC(gt)
Do đó: HM//AB(Định lí 1 từ vuông góc tới song song)
Đúng 1
Bình luận (0)
4 tháng 5 2023 lúc 21:52
Cho tam giác MNP vuông tại M, đường cao MH a) chứng minh tam giác HNM đồng dạng tam giác MNP b) chứng minh hệ thức MH²= NH.PH c) Lấy điểm E tùy ý trên cạnh MP ( E khác M,P) .vẽ điểm F trên cạnh MN sao cho góc FHE = 90°. Chứng minh tam giác NFH đồng dạng tam giác MEH và góc NMH = góc FEH. d) xác định vị trí của điểm E trên MP sao cho diện tích tam giác HÈ đạt giá trị nhỏ nhất
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP
Đúng 1
Bình luận (0)
cho tam giác MNP vuông tại M có cạnh MN<MP. Vẽ đường cao MH, từ H kẻ HL vuông gác với MN tại L. Trên tia HL lấy điểm K sao cho L là trung điểm của HK (vẽ hình giúp mình :((( )
a) Chứng Minh tam giác MHL= tam giác MKL
b) Chứng minh tam giác MKN là tam giác vuông
c) Hãy so sánh các cạnh của tam giác MKN
a: Xét ΔMHL vuông tại L và ΔMKL vuông tại L có
ML chung
HL=KL
Do đó: ΔMHL=ΔMKL
b: Xét ΔMHN và ΔMKN có
MH=MK
\(\widehat{HMN}=\widehat{KMN}\)
MN chung
Do đó; ΔMHN=ΔMKN
Suy ra: \(\widehat{MHN}=\widehat{MKN}=90^0\)
hay ΔMKN vuông tại K
Đúng 3
Bình luận (0)
Mn giúp mình với Cho hình vẽ như trên hình: có AC=BD; ABD=BAC Chứng minh: ∆ABD=∆BAC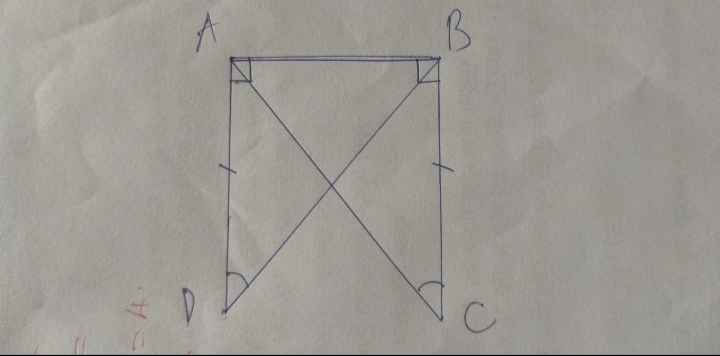
Xét \(\Delta ABD\) và \(\Delta BAC\) có :
AC = BD ( giả thiết )
\(\widehat{ABD}=\widehat{BAC}\) ( giả thiết )
AB chung ( giả thiết , theo hình vẽ )
=> \(\Delta ABD=\Delta BAC\) ( theo trường hợp cạnh - góc - cạnh)
=> điều phải chứng minh
Đúng 1
Bình luận (2)
Cho xOy < 90o có Oz là tia phân giác. Từ điểm M trên tia Oz, vẽ một đường thẳng song song với Oy cắt Ox tại A. Từ M vẽ đường thẳng song song Ox, cắt Oy tại B.
a) Chứng minh: OA = OB
b) Vẽ MH vuông góc Ox tại H , MK vuông góc Oy tại K. Chứng minh : MH = MK
c) Chứng minh OM là trung trực của AB
cho tam giác ABC cân tại A. Gọi M là trung điểm của BC và H là hình chiếu vuông góc của M trên AB. Vẽ đường tròn ( M; MH ), Chứng minh AC tiếp xúc với (M)
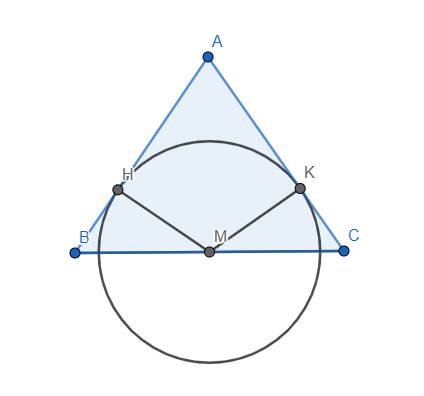
Gọi K là hình chiếu của M lên AC. Xét tam giác MBH vuông tại H và MCK vuông tại K, ta có:
\(MB=MC\) (M là trung điểm BC); \(\widehat{B}=\widehat{C}\) (tam giác ABC cân tại A)
\(\Rightarrow\Delta MBH=\Delta MCK\left(ch-gn\right)\) \(\Rightarrow MH=MK\)
Ta thấy MK chính là khoảng cách từ AC đến M, đồng thời MK bằng MH là bán kính của đường tròn (M; MH) nên AC tiếp xúc với (M) (đpcm)
Đúng 3
Bình luận (0)
Cho thí nghiệm như hình vẽ: Thí nghiệm trên chứng minh tính chất gì của NH3? A. 0,46 B. 0,32 C. 0,34 D. 0,22
Đọc tiếp
Cho thí nghiệm như hình vẽ:
Thí nghiệm trên chứng minh tính chất gì của NH3?
A. 0,46
B. 0,32
C. 0,34
D. 0,22
Cho thí nghiệm như hình vẽ: Thí nghiệm trên chứng minh tính chất gì của NH3? A. Tính bazơ B. Tính axit C. Tính tan D. Khả năng tác dụng với nước
Đọc tiếp
Cho thí nghiệm như hình vẽ:
Thí nghiệm trên chứng minh tính chất gì của NH3?
A. Tính bazơ
B. Tính axit
C. Tính tan
D. Khả năng tác dụng với nước