tập xác định của hàm số:
\(\sqrt{1-sin2x}\) - \(\sqrt{1+sin2x}\)
c1 tập xác định của hàm số \(y=\dfrac{sin2x+cosx}{tanx-sinx}\)
c2 tập xác định của hàm số \(y=\sqrt{1+cot^22x}\)
c3 tập xác định của hàm số \(y=cot\left(x-\dfrac{\pi}{4}\right)+tan\left(x-\dfrac{\pi}{4}\right)\)
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
câu 2 ..... \(\dfrac{cos^22x}{sin^22x}=cot^22x\) nên suy ra sin2x khác 0 đúng hơm
còn câu 3, tui ko hiểu chỗ sin(2x-pi/4).. sao ở đây rớt xuống dợ
Câu 1: tìm tập xác định D của hàm số:
a) y=\(\sqrt{1-sin2x}\)-\(\sqrt{1+sin2x}\)
b) y=\(\sqrt{5+2cot^2x-sinx}\)+ \(cot\left(\frac{\pi}{2}+x\right)\)
c) y=\(tan\left(\frac{\pi}{2}cosx\right)\)
Tìm tham số m để hàm số sau xác định trên R
1/ \(y=\sqrt{cos^2x+cosx-2m+1}\)
2/ \(y=\sqrt{cos2x-2cosx+m}\)
3/ \(y=\sqrt{sin^4x+cos^4x-sin2x-m}\)
1/ Để hàm số y = √cos^2(x) + cos(x) - 2m + 1 xác định trên R, ta cần điều kiện để biểu thức trong căn dương: cos^2(x) + cos(x ) - 2m + 1 > 0 Để giải phương trình này, ta sử dụng một số phép biến đổi: cos^2(x) + cos(x) - 2m + 1 = (cos(x) + 2)(cos(x) - m + 1) Điều kiện để biểu thức trên dương là: cos(x) + 2 > 0 và cos(x) - m + 1 > 0 Với cos(x) + 2 > 0, ta có -2 < cos( x) < 0 Với cos(x) - m + 1 > 0, ta có m - 1 < cos(x) < 1 Tổng Hàm, để hàm số y = √cos^2(x) + cos(x) - 2m + 1 xác định trên R, tham số m phải đáp ứng điều kiện -2 < cos(x) < 0 và m - 1 < cos(x) < 1. 2/ Để hàm số y = √cos^2(x) - 2cos(x) + m xác định trên R, ta cần điều kiện để biểu thức trong căn dương: cos^2(x) - 2cos(x) + m > 0 Đây là một phương trình bậc hai theo cos(x). Để giải phương trình này, ta sử dụng công thức delta: Δ = b^2 - 4ac Ở đây, a = 1, b = -2, c = m. Ta có: Δ = (-2)^2 - 4(1)(m) = 4 - 4m = 4(1 - m) Để phương trình có nghiệm thì Δ > 0. Tức là 1 - m > 0 hay m < 1. Tổng quát, để hàm số y = √cos^2(x) - 2cos(x) + m xác định trên R, tham số m phải đáp ứng m < 1. 3/ Để hàm số y = √sin^ 4 (x) + cos^4(x) - sin^2(x) - m xác định trên R, ta cần điều kiện để biểu thức trong căn dương: sin^4(x) + cos^4(x) - sin ^2(x) - m > 0 Đây cũng là một phương trình bậc hai theo sin(x). Ta sử dụng công thức delta as on, with a = 1, b = -1, c = -m. Δ = (-1)^2 - 4(1)(-m) = 1 + 4m = 4m + 1 Để phương trình có nghiệm thì Δ > 0. Tức là m > -1/4. Tổng quát, để hàm số y = √sin^4(x) + cos^4(x) - sin^2(x) - m xác định trên R, tham số m phải thỏa mãn m > -1/4.
Giải pt:
1. (\(\sqrt{9-x^2}\)-2x).(x\(^3\)+x\(^2\)-12x+10)=0 2. cos3x+2cos\(^2\)(x+\(\dfrac{\pi}{6}\))=1
Bài 2 Tìm tập xác định của hàm số y = \(\dfrac{\sqrt{1-sin2x}}{cos3x}\)
Bài 3 : cho pt (cosx+1)(cos-2x-mcosx)=msin\(^2\) x
tìm m để pt có đúng 2 nghiệm phân biệt thuộc \([0;\dfrac{2\pi}{3}\)\(]\)
bài 4: cho hàm số y= x\(^3\)-2mx\(^2\)+(7m-8)x-5m=10 có đồ thị (C\(_m\)) và đường thẳng d: y=x+m. tìm m để d cắt ( C\(_m\)) tai ba điểm phân biêt
giúp e với mn ơiiii
Tìm m để hàm số \(y=\sqrt{\dfrac{sin2x-cos2x+m-1}{6\left(cos^4x+sin^4x\right)+cos8x+7-5m}}\) xác định với mọi số thực x
\(y=\sqrt{\dfrac{\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1}{2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m}}\)
Hàm xác định trên R khi:
TH1: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\ge0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m>0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}-m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m< \min\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=\dfrac{327}{32}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ge1+\sqrt{2}\\m< \dfrac{327}{160}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Th2: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\le0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m< 0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m>\max\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=14\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le-1-\sqrt{2}\\m>\dfrac{14}{5}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Với giá trị nào của m thì hàm số y = \(m\sqrt{sin2x}\) và hàm số cosx - 1 có cùng tập giá trị.
Giúp e vs ạ!!!!!
\(y=cosx-1\) có tập giá trị \(\left[-2;0\right]\)
- Với \(m>0\)
\(\Rightarrow\) \(y=m\sqrt{sin2x}\) có tập giá trị \(\left[0;m\right]\)
Để 2 hàm có cùng tập giá trị \(\Rightarrow\left\{{}\begin{matrix}-2=0\\0=m\end{matrix}\right.\) ko có m thỏa mãn
- Với \(m\le0\)
\(\Rightarrow y=m\sqrt{sin2x}\) có tập giá trị \(\left[m;0\right]\)
Để 2 hàm có cùng tập giá trị \(\Rightarrow\left\{{}\begin{matrix}m=-2\\0=0\end{matrix}\right.\) \(\Rightarrow m=-2\)
Vậy \(m=-2\)
Tập xác định của hàm số y = 2 x 1 - sin 2 x là
A. R
![]()
![]()
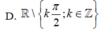
Cho các hàm số i : y = x ; i i : y = x + 1 ; i i i : y = 1 1 + sin 2 x
Có tất cả bao nhiêu hàm số có đạo hàm trên tập xác định của chúng?
A. 0
B. 2
C. 1
D. 3
Tìm tập xác định của hàm số sau: y=sin2x+cos2x
\(y=sin2x+cos2x\)
Vì \(sinx,cosx\) xác định với mọi \(x\in R\) nên hàm số \(y=sin2x+cos2x\) xác định \(\forall x\in R\)
Vậy \(D=R\)