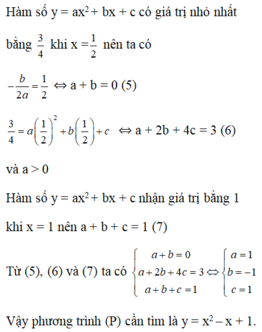Tìm các hệ số b,c của đa thức P(x)=x2+bx+c biết P(x) có giá trị nhỏ nhất bằng -1 khi x=2

Những câu hỏi liên quan
Tìm các hệ số b,c của đa thức P(x)=x2+bx+c biết P(x) có giá trị nhỏ nhất bằng -1 khi x=2
\(P\left(x\right)=\left(x^2+2.\frac{b}{2}x+\frac{b^2}{4}\right)+c-\frac{b^2}{4}=\left(x+\frac{b}{2}\right)^2+c-\frac{b^2}{4}\ge c-\frac{b^2}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=\frac{-b}{2}\)
Mà min P(x)=-1 khi x=2 \(\Rightarrow\)\(\hept{\begin{cases}\frac{-b}{2}=2\\c-\frac{b^2}{4}=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}b=-4\\c=3\end{cases}}\)
\(\Rightarrow\)\(P\left(x\right)=x^2-4x+3\)
Đúng 0
Bình luận (0)
Tìm các hệ số b,c của đa thức p(x)=x2+bx+c, biết P(x) có giá trị nhỏ nhất = -1 khi x=2
Xác định các hệ số a b c để hàm số y=ax2+bx+c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng 1 khi x =1
Cho đa thức P(x)=x3 +ax2 +bx+c
a) Tím các hệ số của a, b, c của đa thức P(x), biết rằng khi x lần lượt nhận các giá trị 1,2; 2,5; 3,7 thì P(x) có giá trị tương ứng là 1994,728; 2060,625; 2173,653
b) Tìm số dư r của phép chia đa thức P(x) cho 2x + 5
c) Tìm giá trị của x khi P(x) có giá trị 1989
SỬ DỤNG MÁY TÍNH FX-570 VN PLUS ĐỂ TÍNH
1,Tìm các hệ số AB của đa thức f(x) = ax + b, biết : f(1)=1; f(2)=4
2, cho đa thứcf(x) : ax mũ 2 + bx + c = 0 ( vs mọi giá trị x ) . CMR : a=b=c=0
3, Cho đa thức f(x) thỏa mãn, f(x) + x. f(-x) = x+1 vs mọi giá trị của x. Tính f(1)
Xác định parabol (P): y a
x
2
+ bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng
3
4
khi x
1
2
và nhận giá trị bằng 1 khi x 1. A. y −
x
2
+ x + 1 B. y
x
2
+ x – 1 C. y
x
2
- x + 2 D. y...
Đọc tiếp
Xác định parabol (P): y = a x 2 + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng 3 4 khi x= 1 2 và nhận giá trị bằng 1 khi x = 1.
A. y = − x 2 + x + 1
B. y = x 2 + x – 1
C. y = x 2 - x + 2
D. y = x 2 - x + 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của đa thức f(x)=ax^2+bx+c (a,b,c là các số cho trước và a khác 0)
1. Cho a + b 1. Tìm giá trị nhỏ nhất của biểu thức : M a3 + b3.2. Cho a3 + b3 2. Tìm giá trị lớn nhất của biểu thức : N a + b.3. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)4. Tìm liên hệ giữa các số a và b biết rằng: a b a b 5. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4ab) Cho a, b, c 0 và abc 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 86. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)7. Tìm các giá trị của x sao cho:a) | 2...
Đọc tiếp
1. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức : M = a3 + b3.
2. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức : N = a + b.
3. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
4. Tìm liên hệ giữa các số a và b biết rằng: a b a b
5. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
6. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
7. Tìm các giá trị của x sao cho:
a) | 2x – 3 | = | 1 – x | b) x2 – 4x ≤ 5 c) 2x(2x – 1) ≤ 2x – 1.
8. Tìm các số a, b, c, d biết rằng : a2 + b2 + c2 + d2 = a(b + c + d)
9. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của avà b thì M đạt giá trị nhỏ nhất ? Tìm giá trị nhỏ nhất đó.
10. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. CMR giá trị nhỏ nhất của P bằng 0.
11. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau :
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
Đúng 0
Bình luận (0)
bạn nên viết ra từng câu
Chứ để như thế này khó nhìn lắm
Đúng 0
Bình luận (0)
bạn hỏi từ từ thôi
Cho đa thức f(x)=(x2 - bx) (2x + b) có hệ số của x2 là 5, tìm giá trị của f(1)
f(x) = (x² - bx)(2x + b)
= 2x³ + bx² - 2bx² - b²x
= 2x³ - bx² - b²x
Do hệ số của x² là 5
⇒ -b = 5
⇒ b = -5
f(x) = 2x³ + 5x² - 25x
f(1) = 2.1³ + 5.1² - 25.1
= -18
Đúng 2
Bình luận (0)