a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

\(\widehat{B}\) chung

Do đó:ΔABH\(\sim\)ΔCBA

b: Xét ΔABC vuông tại A có AH là đường cao

nên \(AC^2=CH\cdot CB\)(hệ thức lượng)

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

góc B chung

=>ΔABH đồng dạng với ΔCBA

b: ΔABC vuông tại A

mà AH là đường cao

nên HA^2=HB*HC

c: AI/IH=BA/BH

EC/AE=BC/BA

mà BA/BH=BC/BA

nên AI/IH=EC/AE
=>AI*AE=IH*EC

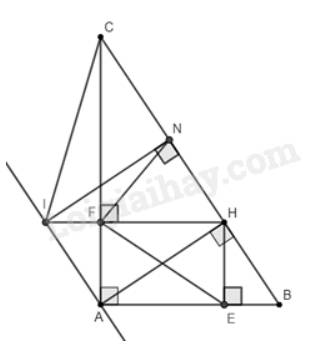
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)

Xét tam giác \(ABH\) và tam giác \(CBA\) có:

\(\widehat B\) (chung)

\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).

Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{B^2} = BH.BC\) .

b)

-  Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)

Xét tam giác \(AHE\) và tam giác \(ABH\) có:

\(\widehat {HAE}\) (chung)

\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).

Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AB.AE\) . (1)

- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)

Xét tam giác \(AHF\) và tam giác \(ACH\) có:

\(\widehat {HAF}\) (chung)

\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).

Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AF.AC\) . (2)

Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)

c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).

Xét tam giác \(AFE\) và tam giác \(ABC\) có:

\(\widehat A\) (chung)

\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)

Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).

d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).

Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).

Xét tam giác \(HFC\) và tam giác \(HNI\) có:

\(\widehat {CHI}\) (chung)

\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).

Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)

Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).

Xét tam giác \(HNF\) và tam giác \(HIC\) có:

\(\widehat {CHI}\) (chung)

\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)

Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).

2:

a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

góc HAB=góc HCA

=>ΔHAB đồng dạng với ΔHCA

=>HA/HC=HB/HA

=>HA^2=HB*HC

b: BC=4+9=13cm

AH=căn 4*9=6cm

S ABC=1/2*6*13=39cm²

Hình bạn tự vẽ nhé

a) Xét ΔABH và ΔCBA có :

^AHB = ^A = 90⁰

^B chung

=> ΔABH ~ ΔCBA (g.g)

b) Vì ΔABC vuông tại A, áp dụng định lí Pythagoras ta có :

\(BC^2=AB^2+AC^2\)

<=> \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét ΔABC có BD là phân giác của ^B nên theo tính chất đường phân giác trong tam giác ta có : \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\)

Theo tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{AD}{AB}=\dfrac{DC}{BC}=\dfrac{AD+DC}{AB+BC}=\dfrac{AC}{AB+BC}=\dfrac{8}{6+10}=\dfrac{1}{2}\)

=> \(\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{1}{2}\\\dfrac{DC}{BC}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=\dfrac{1}{2}AB=3cm\\DC=\dfrac{1}{2}BC=5cm\end{matrix}\right.\)

c) Xét ΔABD và ΔHBI có :

^A = ^BHI = 90⁰ 

^ABD = ^HBI ( do BD là phân giác của ^B )

=> ^ABD ~ ΔHBI (g.g)

=> \(\dfrac{AB}{HB}=\dfrac{BD}{BI}=\dfrac{AD}{HI}\)=> AB.BI = HB.BD ( đpcm )

d) Từ \(\dfrac{AB}{HB}=\dfrac{BD}{BI}=\dfrac{AD}{HI}\)=> \(\dfrac{AB}{AD}=\dfrac{BD}{BI}=\dfrac{HB}{HI}=2\)

Ta có : \(S_{ABD}=\dfrac{1}{2}AB\cdot AD=\dfrac{1}{2}\cdot6\cdot3=9cm^2\)

mà ta có \(\dfrac{S_{ABD}}{S_{HBI}}=2^2=4\)=> S_ABD = 4S_HBI

<=> 9 = 4S_HBI <=> S_HBI = 9/4cm²