choΔABC vuông tại a,AH⊥BC.Biết AB=6cm,HC=5cm.Tính AH,phân giác AD

Những câu hỏi liên quan
cho tam giác abc vuông tại a đường cao ah, phân giác AD; AH=6cm; HB=4cm
a) tính HC ,BC, AB ,AC
b) tính BD, CD
cho tam giác ABC vuông tại A vẽ đường cao AH,H thuốc BC.biết AB=6cm,AC= 8cm a. chứng minh tam giác HBA đồng dạng với với tam giác ABC b. tính BC,AH,BH c. kẻ HI vuông góc với AC tại I chứng minh HC^2=IC*AC
a, Xét tam giác HBA và tam giác ABC có
^B _ chung ; ^BHA = ^BAC = 900
Vậy tam giác HBA ~ tam giác ABC (g.g)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}cm\)
\(\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
b, Xét tam giác CHI và tan giác CAH có
^AIH = ^CHA = 900
^C _ chung
Vậy tam giác CHI ~ tam giác CAH (g.g)
\(\dfrac{CH}{AC}=\dfrac{CI}{CH}\Rightarrow CH^2=CI.AC\)
Đúng 2
Bình luận (0)
1,Cho tam giác ABC vuông tại A.Vẽ AH vuông góc với BC.Biết AH=1cm.CMR:BC^2=HB^2+HC^2+2
2,Cho tam giác ABC vuông tại A,AB=7cm;BC=11 cm.Vẽ các cung tròn tâm A và tâm C cùng bán kính 6cm,chúng cắt nhau tại M.Tính số đo các góc của tam giác MAC
Giúp mk với ạk!!Thank nhìu
Bài 1. Chi tam giác ABC vuông tại A phân giác AD, đường cao AH biết CD= 68cm, BD=51cm. Tính BH,HC
Bài 2 . Cho tam giác ABC vuông tại A đường cao AH biết AB=7,5cm, AH=6cm.
a, Tính AC,BC
b, Tính Cos B, Cos C
Bài 1:
\(BC=CD+BD=68+51=119\)
\(AD\)là phân giác \(\widehat{BAC}\)\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay \(\frac{51}{AB}=\frac{68}{AC}\)
\(\Leftrightarrow\)\(\frac{51^2}{AB^2}=\frac{68^2}{AC^2}=\frac{51^2+68^2}{AB^2+AC^2}=\frac{25}{49}\)
suy ra: \(\frac{51^2}{AB^2}=\frac{25}{49}\)\(\Rightarrow\)\(AB=71,4\)
ÁP dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Leftrightarrow\)\(BH=\frac{AB^2}{BC}=\frac{71,4^2}{119}=42,84\)
\(\Rightarrow\)\(CH=BC-BH=119-42,84=76,16\)
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow\)\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(BH^2=7,5^2-6^2=20,25\)
\(\Leftrightarrow\)\(BH=4,5\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}=\frac{7,5^2}{4,5}=12,5\)
\(AB.AC=BC.AH\)
\(\Rightarrow\)\(AC=\frac{BC.AH}{AB}=\frac{12,5.6}{7,5}=10\)
b) \(cosB=\frac{AC}{BC}=\frac{10}{12,5}=0.8\)
\(cosC=\frac{AB}{BC}=\frac{7,5}{12,5}=0,6\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông ở A có AC=20cm,kẻ AH vuông góc với BC.Biết BH=9CM,HC=16CM.Tính AB,AH
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
Đúng 2
Bình luận (1)
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
Đúng 2
Bình luận (1)
Ta có :
BC = BH + HC
=> BC = 9 + 16
=> BC = 25 (cm)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+BC^2\) (định lí Py - ta - go)
=> \(25^2=AB^2+20^2\)
=> \(AB^2=225\)
=> AB = 15 (cm)
Xét Δ ABH vuông tại H, có :
\(AB^2=BH^2+AH^2\) (định lí Py - ta - go)
=> \(15^2=9^2+AH^2\)
=> \(AH^2=144\)
=> AH = 12 (cm)
Đúng 1
Bình luận (1)
cho tam giác ABC vuông tại A có AC=20cm.Kẻ AH vuông góc với BC.Biết BH=9cm,HC=16cm.Tính độ các cạnh góc vuông AB và AC
help meee
Cho tam giác ABC vuông tại A: AB = 6cm, AC = 8cm. Kẻ phân giác trong
BD của góc ABC (D thuộc AC).
a) Tính AD, CD b) Vẽ đường cao AH. Tính AH, HC
c) Tia phân giác góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh
BIM là góc vuông
a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)
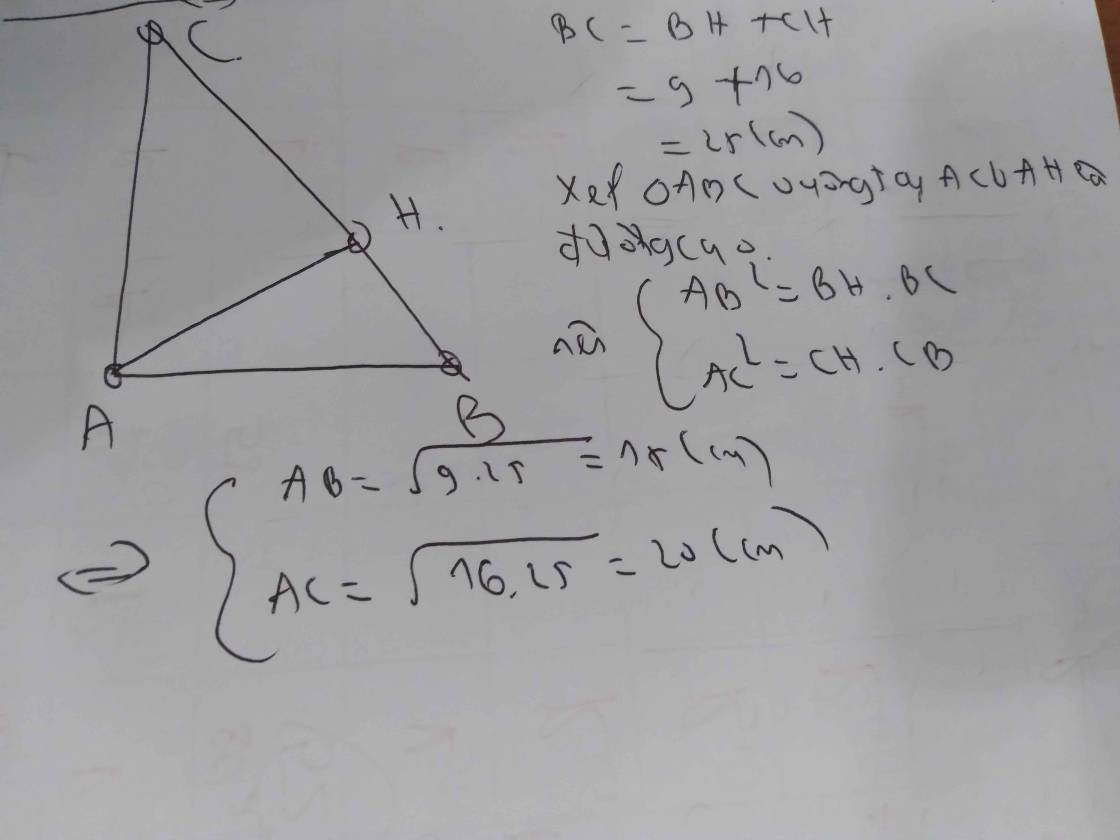
cho ABC vuông tại A có AB=30cm.Kẻ AH vuông góc với BC.Biết AH=24cm,BC=50cm.Tính độ dài cạnh AC,BH và HC?
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=50^2-30^2=1600\)
=>AC=40(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(BH=\dfrac{30^2}{50}=18\left(cm\right);CH=\dfrac{40^2}{50}=32\left(cm\right)\)
Đúng 3
Bình luận (0)
Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=50^2-30^2=1600\Rightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABH\) vuông tại H ta có: \(AH^2+BH^2=AB^2\Rightarrow24^2+BH^2=30^2\Rightarrow BH^2=30^2-24^2=324\Rightarrow BH=\sqrt{324}=18\left(cm\right)\)\(HC=BC-BH=50-18=32\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH, gọi I,K lần lượt là trung điểm của HC, AC. Chứng minh: a. HD//AC và HC là đường phân giác của góc KHD. b. AH+HC>2AI c. Tính AH, biết AB= 6cm, AC=8cm