Cho phương trình
x4-4x3+8x=m. Xác định m để phương trình có 4 nghiệm phân biệt
Những câu hỏi liên quan
Xác định m để phương trình
m
x
2
-
6
x
-
7
có 4 nghiệm phân biệt. A. m ∈ (−16; 16). B. m ∈ (0; 16) C. m ∈ ∅. D. m ∈ [0; 16].
Đọc tiếp
Xác định m để phương trình m = x 2 - 6 x - 7 có 4 nghiệm phân biệt.
A. m ∈ (−16; 16).
B. m ∈ (0; 16)
C. m ∈ ∅.
D. m ∈ [0; 16].
m = x 2 - 6 x - 7 là phương trình hoành độ giao điểm của đường thẳng y = m và đồ thị (C): y = x 2 - 6 x - 7
Vẽ (P): y = x 2 - 6 x - 7 , lấy đối xứng phần phía dưới Ox của (P) lên trên Ox và xóa đi phần phía dưới Ox (vì y = x 2 - 6 x - 7 , ∀ x ∈ R ), ta được đồ thị (C).
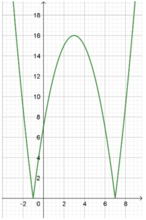
Dựa vào đồ thị: phương trình m = x 2 - 6 x - 7 có 4 nghiệm phân biệt khi m ∈ 0 ; 16 .
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Câu 2: Cho phương trình x2 + 4x + m +1 = 0 . Xác định m để phương trình a) Vônghiệm b) Cónghiệmkép c) Cónghiệm d) Có hai nghiệm phân biệt e) Có hai nghiệm trái dấu f) Có hai nghiệm dương phân biệt
Pt: x2+4x+m+1 (1)
Ta có △'= 22-1.(m+1)=3-m
a) Pt (1) vô nghiệm ⇔△'<0⇔3-m<0⇔m>3
b) (1) có nghiệm kép ⇔△'=0 ⇔ m=3
c) (1) có nghiệm ⇔ △' ≥ 0 ⇔ m ≤3
d) (1) có 2 nghiệm phân biệt ⇔ △' >0 ⇔m<3
e) (1) có 2 nghiệm trái dấu ⇔ 1.(m+1)< 0⇔m<-1
f) (1) có 2 nghiệm dương phân biệt ⇔ △'>0 , x1+x2 = -b/a>0, x1.x2=c/a>0
⇔m<3, -4>0, m+1>0
⇒ vô nghiệm
Đúng 0
Bình luận (0)
Cho phương trình \(x^2-8x-3\left(m-1\right)=0\)
a) Tìm m để phương trình có hai nghiệm phân biệt nhỏ hơn 7
b) Tìm m để phương trình có hai nghiệm phân biệt lớn hơn 7.
c) Tìm m để phương trình có hai nghiệm thỏa mãn \(x_1< 7< x_2\)
\(\text{Δ}=\left(-8\right)^2-4\cdot\left(-3\right)\cdot\left(m-1\right)\)
\(=64+12\left(m-1\right)\)
=64+12m-12
=12m+52
a: Để phương trình có hai nghiệm phân biệt nhỏ hơn 7 thì
\(\left\{{}\begin{matrix}12m+52>0\\8< 14\end{matrix}\right.\Leftrightarrow m>-\dfrac{13}{4}\)
b: Để phương trình có hai nghiệm phân biệt lớn hơn 7 thì \(\left\{{}\begin{matrix}12m+52>0\\8>14\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
Cho phương trình x 2 – 4x = 2|x – 2| − m – 5, với m là tham số. Xác định m để phương trình có bốn nghiệm phân biệt
A. m < 1
B. −1 < m < 0
C. 0 < m < 1
D. m > 0
Cho phương trình: x²-2(m-3)x+(m-4)=0 (1) a) giải phương trình với m=1 b) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt c) Xác định m để phương trình có hai nghiệm trái dấu d)Tính theo m giá trị của biểu thức A=1/x1+1/x2.Tìm m để A € Z để A € Z
a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4
Đúng 0
Bình luận (0)
Cho phương trình x^2 -(m-1)x-m=0 Xác định giá trị của m để phương trình có 2 nghiệm phân biệt bé hơn 1
\(\Delta=\left(m-1\right)^2-4.\left(-m\right)\)
\(=\left(m^2-2m+1\right)+4m=\left(m+1\right)^2\)
Để pt có 2 nghiệm phân biệt => \(m\ne-1\)
\(\left[{}\begin{matrix}x_1=\dfrac{m-1+m+1}{2}=m\\x_2=\dfrac{m-1-m-1}{2}=-1\end{matrix}\right.\)
Để pt có 2 nghiệm phân biệt bé 1
\(\Rightarrow m< 1\)
Đúng 1
Bình luận (0)
Ta có: `{(x_1 < 1),(x_2 < 1):}=>(x_1 -1)(x_2 -1) > 0`
Phương trình có `2` nghiệm phân biệt
`=>\Delta > 0`
`<=>[-(m-1)]^2+4m > 0`
`<=>m^2-2m+4m+1 > 0`
`<=>m^2+2m+1 > 0<=>(m+1)^2 > 0`
`=>m+1 ne 0<=>m ne -1`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=m-1),(x_1.x_2=c/a=-m):}`
Ta có: `(x_1 -1)(x_2 -1) > 0`
`<=>x_1 .x_2-(x_1 +x_2)+1 > 0`
`<=>-m-m+1+1 > 0`
`<=>m < 1`
Mà `m ne -1`
`=>m < 1,m ne -1`.
Đúng 1
Bình luận (0)
Tìm các giá trị của m để phương trình
3
x
-
4
x
3
m
có ba nghiệm phân biệt.
Đọc tiếp
Tìm các giá trị của m để phương trình 3 x - 4 x 3 = m có ba nghiệm phân biệt.
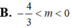
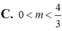
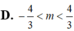
cho phương trình x^2-(m+3)x + m+2=0 với m là tham số a) hãy tìm điều kiện của m để phương trình đã cho có 2 nghiệm trái dấu b) xác định m để phương trình đã cho có 2 nghiệm phân biệt x1,x2 thoả mãn x1=3x2
a: Để phương trình có hai nghiệm trái dấu thì m+2<0
hay m<-2
Đúng 0
Bình luận (0)
Cho phương trình: x^2-left(2m-3right)x+m^2-3m0
a) CMR phương trình luôn có hai nghiệm phân biệt với mọi m
b) Xác định m để phương trình có hai nghiệm x_1,x_2 thoả mãn 1 x_1 x_2 6
Đọc tiếp
Cho phương trình: \(x^2-\left(2m-3\right)x+m^2-3m=0\)
a) CMR phương trình luôn có hai nghiệm phân biệt với mọi m
b) Xác định m để phương trình có hai nghiệm \(x_1,x_2\) thoả mãn \(1< x_1< x_2< 6\)
a) Xét pt \(x^2-\left(2m-3\right)x+m^2-3m=0\)
Ta có \(\Delta=\left[-\left(2m-3\right)^2\right]-4.1\left(m^2-3m\right)\)\(=4m^2-12m+9-4m^2+12m\)\(=9>0\)
Vậy pt đã cho luôn có 2 nghiệm phân biệt với mọi m.
Câu b mình nhìn không rõ đề, bạn sửa lại nhé.