Cho hình bình hành ABCD.Gọi E là trung điểm của AD,F là trung điểm của BC.CMR:BE=DF

Những câu hỏi liên quan
cho hình bình hành ABCD.gọi E là trung điểm của AD, F là trung điểm của BC. a chứng minh tứ giác EBDF là hình bình hành
a) E là trung điểm của AD
F là trung điểm của BC
mà AD = BC (ABCD là hình bình hành)
nên AE = CF
Xét tam giác ABE và tam giác CDF có
góc A = góc C (ABCD là hình bình hành)
AB = CD (ABCD là hình bình hành)
AE = CF (cmt)
Suy ra tam giác ABE = tam giác ACF (cgc)
\(\Rightarrow\) góc E1 = góc F1
mà góc D1 = góc F1 (AD//BC,ABCD là hình bình hành)
nên góc E1 = góc D1
mà 2 góc này có vị trí đồng vị nên EB // DF
Tứ giác EBFD có EB // DF (cmt)
ED // BF (AD // BC, ABCD là hình bình hành)
\(\Rightarrow\) EBFD là hình bình hành
Đúng 0
Bình luận (0)
cho hình thang ABCD.Gọi E là trung điểm của AD,F là trung điểm của BC.Chứng Minh rằng BE=DF
ABCD là hình bình hành nên AB =CD (cạnh đối của hình bình hành) (1)
F là trung điểm của BC (theo đầu bài) nên BF = 1/2 BC (2).
E là trung điểm của AD (theo đầu bài) nên ED = 1/2 AD (3).
Từ (1), (2) và (3) suy ra BF = ED (4).
BF // ED (vì F nằm trên AB, E nằm trên AD; BC và AD là cạnh đối của hình bình hành ABCD nên BC//AD) (5).
Từ (4) và (5) suy ra BFDE là hình bình hành (2 cạnh đối song song và bằng nhau) =>BE = DF (điều phải chứng minh)
đúng hông
Đúng 0
Bình luận (0)
Cho tứ giác ABCD.Gọi E là trung điểm của AD,F là trung điểm của AB,L là trung điểm của DC,K là trung điểm của BC.Trong các khẳng định sau, khẳng định nào là đúng ?
A.Tứ giác EFBD là hình bình hành
B.Tứ giác EFKL là hình bình hành
C.Tứ giác ACLE là hình bình hành
D.Tứ giác DBKL là hình bình hành
Cho tứ giác ABCD.Gọi E là trung điểm của AD,F là trung điểm của AB,L là trung điểm của DC,K là trung điểm của BC.Trong các khẳng định sau, khẳng định nào là đúng ?
A.Tứ giác EFBD là hình bình hành
B.Tứ giác EFKL là hình bình hành
C.Tứ giác ACLE là hình bình hành
D.Tứ giác DBKL là hình bình hành
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF
Cách 1:
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = AD/2
F là trung điểm của BC ⇒ CF = BC/2
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF.
Cách 2:
ABCD là hình bình hành ⇒ AD//BC và AD = BC.
+ AD // BC ⇒ DE // BF
+ E là trung điểm của AD ⇒ DE = AD/2
F là trung điểm của BC ⇒ BF = BC/2
Mà AD = BC ⇒ DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF ?
Bài giải:
Tứ giác BEDF có:
DE // BF ( vì AD // BC)
DE = BF \(\left(DE=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BF\right)\)
Nên BEDF là hình bình hành.
Suy ra BE = DF.
Đúng 0
Bình luận (0)
Xét \(\Delta ABF\) và \(\Delta CDE\) có :
\(AB=CD\left(gt\right)\)
Góc \(A\) \(=\) Góc \(B\) \((gt)\)
\(AE=CF\left(=\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Vậy \(\Delta ABE=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow BE=DF\) (2 cạnh tương ứng)
P/s : Đây là lần đầu em vẽ hình trên máy nên dễ sai sót ạ,với lại em khong thấy kí hiệu góc ở đâu ạ :v Thông cảm cho em
Đúng 0
Bình luận (6)
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và A B E ^ = C D F ^ .
Xét tứ giác BEDF có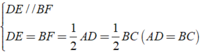
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
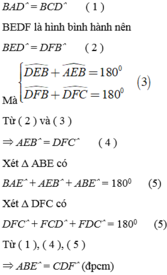
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD.gọi E là trung điểm của AD,Flà trung điểm của BC . Chứng minh rằng :BE=DE
cho hình bình hành abcd, gọi e là trung điểm ad, f là trung điểm bc. cmr DEBF là hình bình hành. cmr: DE =DF
Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.
a) Chứng minh BE=DF và góc ABE = góc CDF.
b, chứng minh:EB//DF
giúp mình với!
a/ Do ABCD là hình bình hành nên:
- AB=CD; AD=BC
- Mà E là trung điểm của AD, F là trung điểm của BC
=> AE=ED=BF=FC
Xét △ABE và △FCD có:
- AE=CF (cmt)
- Góc BAE = Góc FCD (gt)
- AB=CD (gt)
=> △ABE=△CDF (c.g.c)
Vậy: BE=DF; góc ABE = góc CDF (đpcm)
b/ Ta có:
- BC // AD (gt)
- Tia BF thuộc tia BC, tia DE thuộc tia AD
=> BF // DE
DE = BF (cmt)
=> DEBF là hình bình hành (Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành)
Vậy: EB // DF (đpcm)
Đúng 5
Bình luận (0)



















