tổng tất cả các nghiệm thuộc [0; 2π] của phương trình 2sinx - \(\sqrt{3}\) = 0 là ?
\(2sinx-\sqrt{3}=0\)
\(\Leftrightarrow sinx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(0\le\dfrac{\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{6}\le k\le\dfrac{5}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{\pi}{3}\)
\(0\le\dfrac{2\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{3}\le k\le\dfrac{4}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{2\pi}{3}\)
\(\Rightarrow x_1+x_2=\pi\)
Tổng tất cả các nghiệm của phương trình sin 3 x - 2 3 sin 2 x = 2 sin x cos 2 x thuộc 0 ; π
A. 5 π
B. 6 π
C. 3 π
D. 2 π
Tìm tập nghiệm của phương trình: \(\dfrac{\sqrt[]{3}sin^2x-2sinxcosx-\sqrt{3}cos^2x}{\left(2sinx+3\right)\left(4cos^2x-3\right)}=0\)
ĐKXĐ: \(cos2x\ne\dfrac{1}{2}\Leftrightarrow x\ne\pm\dfrac{\pi}{6}+k\pi\)
\(\sqrt{3}sin^2x-2sinx.cosx-\sqrt{3}cos^2x=0\)
\(\Leftrightarrow-sin2x-\sqrt{3}\left(cos^2x-sin^2x\right)=0\)
\(\Leftrightarrow sin2x+\sqrt{3}cos2x=0\)
\(\Leftrightarrow\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x=0\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow2x+\dfrac{\pi}{3}=k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
Nghiệm này bao gồm 2 họ nghiệm: \(\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Do đó sau khi loại nghiệm theo ĐKXĐ ta được nghiệm của pt là: \(x=\dfrac{\pi}{3}+k\pi\)
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Chọn D.
Phương pháp:
- Sử dụng các công thức nhân ba, phân tích tích thành tổng để biến đổi đơn giản phương trình.
- Giải phương trình, tìm nghiệm thỏa mãn bài toán và tính tổng các nghiệm.
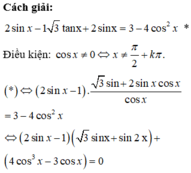
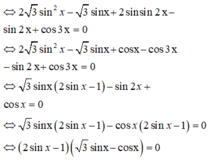
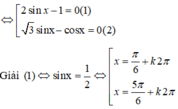
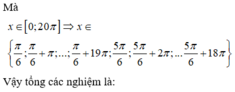
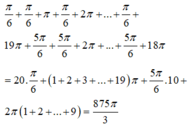
Tổng các nghiệm của phương trình 2 sin x + 2 cos x - 6 sin x - 3 = 0 trên khoảng 0 ; 2 π
A. 3 π
B. 5 π 2
C. 17 π 2
D. 10 π 3
Tìm điều kiện của m để phương trình \(2sinx+m=0\) có đúng 2 nghiệm thuộc đoạn \(\left[0;\pi\right]\)
Cho phương trình
2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Gọi T là tập hợp các nghiệm thuộc đoạn 0 ; 20 π của phương trình trên. Tính tổng các phần tử của T
A. 570 3 π
B. 875 3 π
C. 880 3 π
D. 1150 3 π
Số nghiệm thuộc đoạn 0 ; 2018 π của phương trình cos 2 x - 2 sin x + 3 = 0 là
A. 2017
B. 1009
C. 1010
D. 2018
Tổng các nghiệm của phương trình Sin3x(2Cosx-Sin3) + Cos3x(2Sinx-Cos3x)=0 trên [0,3.14]
