|x^2 -3x-3+m| = x+1 có 4 nghiệm phân biệt . bao nhiểu giá trị nguyên m thỏa

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để pt: (m + 1).25log2(x) + (m - 2)xlog2(5) - 2m + 1 = 0 có 2 nghiệm phân biệt x1, x2 thỏa mãn: x1.x2 = 4
ĐKXĐ: \(x>0\)
\(x^{log_25}=t\Rightarrow25^{log_2x}=\left(5^{log_2x}\right)^2=\left(x^{log_25}\right)^2=t^2\)
\(x_1x_2=4\Rightarrow t_1t_2=\left(x_1x_2\right)^{log_25}=4^{log_25}=25\)
\(\left(m+1\right)t^2+\left(m-2\right)t-2m+1=0\) (1)
Pt có 2 nghiệm pb \(\Rightarrow\) (1) có 2 nghiệm dương pb
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-2\right)^2-4\left(m+1\right)\left(-2m+1\right)>0\\t_1+t_2=\dfrac{2-m}{m+1}>0\\t_1t_2=\dfrac{-2m+1}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\-1< m< \dfrac{1}{2}\end{matrix}\right.\)
Ủa làm đến đây mới thấy kì kì, chỉ riêng hệ điều kiện này đã ko tồn tại m nguyên rồi, chưa cần điều kiện \(x_1x_2=4\)
Đúng 0
Bình luận (1)
\(t=1\) pt có nghiệm kép bạn ơi, ko phải 2 nghiệm pb như đề yêu cầu đâu
Đúng 0
Bình luận (0)
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
Có bao nhiêu giá trị nguyên m để phương trình \(x^2-4\sqrt{x^2+1}-\left(m-1\right)=0\) có 4 nghiệm phân biệt
Điều kiện xác định x∈Rx∈R.
Đặt t=√x2+1 (t≥1t≥1)
Phương trình trở thành t2−1−4t−m+1=0
⇔t2−4t=m
⇔t2−4t=m. (1)
Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.
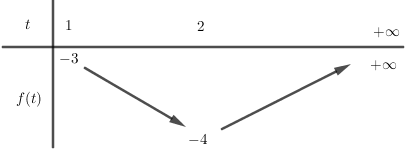
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:
Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3
Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (2)
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Cho phương trình \(x^2-3x+m=0\) (1) (x là ẩn).
Tìm các giá trị m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thỏa mãn \(\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=3\sqrt{3}\).
\(\Delta=9-4m>0\Rightarrow m< \dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m\end{matrix}\right.\)
\(\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=3\sqrt{3}\)
\(\Leftrightarrow x_1^2+x_2^2+2+2\sqrt{\left(x_1^2+1\right)\left(x_2^2+1\right)}=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\sqrt{\left(x_1x_2\right)^2+\left(x_1+x_2\right)^2-2x_1x_2+1}=25\)
\(\Leftrightarrow9-2m+2\sqrt{m^2+9-2m+1}=25\)
\(\Leftrightarrow\sqrt{m^2-2m+10}=m+8\left(m\ge-8\right)\)
\(\Leftrightarrow m^2-2m+10=m^2+16m+64\)
\(\Rightarrow m=-3\) (thỏa mãn)
Đúng 5
Bình luận (1)
Pt trên có a=1, b=5, c=-3m+2
\(\Delta=b^2-4ac=25-4\cdot1\cdot\left(-3m+2\right)=17+12m\)
Để pt có hai nghiệm phân biệt thì \(\Delta>0\)<=> 17+12m >0 <=>m> 17/12
Theo hệ thức Viet, ta có:
\(\hept{\begin{cases}x_1+x_2=-5\\x_1\cdot x_2=-3m+2\end{cases}}\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1\cdot x_2=25-4\left(-3m+2\right)=17+12m=10\)
=> 12m = -7 <=>m=-7/12 (thỏa đkxđ)
Vậy với m=-7/12 thì phương trình có hai nghiệm x1, x2 thỏa (x1 - x2)^2 =10
Đúng 3
Bình luận (0)
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
\(x^2-2mx+2m-3=0\) (1)
tìm giá trị nguyên m nhỏ nhất để (1) có 2 nghiệm phân biệt \(x_{1;}x_2\) thỏa mãn \(9-x_1^2-x^2_2>=0\)
\(\text{Δ}=\left(-2m\right)^2-4\left(2m-3\right)\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\forall m\)
=>Phương trình (1) luôn có hai nghiệm phân biệt
Áp dụng Vi-et, ta được: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-2m\right)}{1}=2m\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
\(9-x_1^2-x_2^2>=0\)
=>\(9-\left(x_1^2+x_2^2\right)>=0\)
=>\(9-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]>=0\)
=>\(9-\left[\left(2m\right)^2-2\left(2m-3\right)\right]>=0\)
=>\(9-4m^2+4m-6>=0\)
=>\(-4m^2+4m+3>=0\)
=>\(4m^2-4m-3< =0\)
=>\(4m^2-6m+2m-3< =0\)
=>(2m-3)(2m+1)<=0
=>\(-\dfrac{1}{2}< =m< =\dfrac{3}{2}\)
mà m là số nguyên nhỏ nhất
nên m=0
Đúng 2
Bình luận (0)
pt: \(x^2-2\left(m-1\right)x+m-3=0\) (m là tham số)
phương trình có hai nghiệm phân biệt tìm giá trị nguyên của m sao cho pt có 2 nghiệm thỏa mãn:
\(\left(\dfrac{1}{x_1}-\dfrac{1}{x_2}\right)^2=\dfrac{\sqrt{11}}{2}\)
Δ=(2m-2)^2-4(m-3)
=4m^2-8m+4-4m+12
=4m^2-12m+16
=4m^2-12m+9+7=(2m-3)^2+7>=7>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(\left(\dfrac{1}{x1}-\dfrac{1}{x2}\right)^2=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}-\dfrac{2}{x_1x_2}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{\left(\left(x_1+x_2\right)^2-2x_1x_2\right)}{\left(x_1\cdot x_2\right)^2}-\dfrac{2}{x_1\cdot x_2}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{\left(2m-2\right)^2-2\left(m-3\right)}{\left(-m+3\right)^2}-\dfrac{2}{-m+3}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{4m^2-8m+4-2m+6}{\left(m-3\right)^2}+\dfrac{2}{m-3}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{4m^2-10m+10+2m-6}{\left(m-3\right)^2}=\dfrac{\sqrt{11}}{2}\)
=>\(\sqrt{11}\left(m-3\right)^2=2\left(4m^2-8m+4\right)\)
=>\(\sqrt{11}\left(m-3\right)^2=2\left(2m-2\right)^2\)
=>\(\Leftrightarrow\left(\dfrac{m-3}{2m-2}\right)^2=\dfrac{2}{\sqrt{11}}\)
=>\(\left[{}\begin{matrix}\dfrac{m-3}{2m-2}=\sqrt{\dfrac{2}{\sqrt{11}}}\\\dfrac{m-3}{2m-2}=-\sqrt{\dfrac{2}{\sqrt{11}}}\end{matrix}\right.\)
mà m nguyên
nên \(m\in\varnothing\)
Đúng 2
Bình luận (0)