Gọi E là giao điểm của hai đường thẳng AB,CD; F là giao điểm của hai đường thẳng AD,BC tứ giác ABCD. Tính góc tạo bởi hai tia phân giác của góc E và góc F theo các góc của tứ giác ABCD.

Những câu hỏi liên quan
.Gọi E là giao điểm của hai đường thẳng AB, CD; F là giao điểm của hai đường thẳng AD, BC của tứ giác ABCD. Tính góc tạo bởi hai tia phân giác của góc E và góc F theo các góc của tứ giác ABCD
cho đường tròn (O,R) hai đường kính AB và CD vuông góc với nhau . Gọi E là điểm thuộc cung nhỏ BC ( E không trùng với B,C) tiếp tuyến của đường tròn (O,R) tại E cắt đường thẳng AB tại I.Gọi F là giao điểm của DE và AB , K là điểm thuộc đường thẳng IE sao cho KF vuông góc với AB) a) chứng minh tứ giác OKEF là tứ giác nội tiếp b)chứng minh góc OKF bằng góc ODF c)chứng minh DE nhân DF bằng 2 nhân R bình phương d)Gọi M là giao điểm của OK vafCF ,tính tan góc MDC khi góc EIB bằng 45độ
Đọc tiếp
cho đường tròn (O,R) hai đường kính AB và CD vuông góc với nhau . Gọi E là điểm thuộc cung nhỏ BC ( E không trùng với B,C) tiếp tuyến của đường tròn (O,R) tại E cắt đường thẳng AB tại I.Gọi F là giao điểm của DE và AB , K là điểm thuộc đường thẳng IE sao cho KF vuông góc với AB) a) chứng minh tứ giác OKEF là tứ giác nội tiếp b)chứng minh góc OKF bằng góc ODF c)chứng minh DE nhân DF bằng 2 nhân R bình phương d)Gọi M là giao điểm của OK vafCF ,tính tan góc MDC khi góc EIB bằng 45độ
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm P không trùng với trung điểm của AD.
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD).
b) Tìm giao điểm của hai mặt phẳng (PMN) và BC.
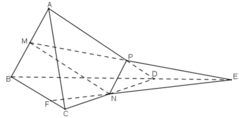
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.
Đúng 1
Bình luận (0)
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

a) \(\Delta \)ABE =\(\Delta \)DCE;
b) EG = EH.
a)Xét hai tam giác ABE và DCE có:
\(\widehat {BAE} = \widehat {CDE}\)(so le trong)
AB=CD(gt)
\(\widehat {ABE} = \widehat {DCE}\)(so le trong)
Vậy \(\Delta \)ABE =\(\Delta \)DCE(g.c.g)
b)Xét hai tam giác BEG và CEH có:
\(\widehat {CEH} = \widehat {BEG}\)(đối đỉnh)
CE=BE (do \(\Delta \)ABE =\(\Delta \)DCE)
\(\widehat {ECH} = \widehat {EBG}\)(so le trong)
Suy ra \(\Delta BEG{\rm{ = }}\Delta CEH\)(g.c.g)
Vậy EG=EH (hai cạnh tương ứng).
Đúng 1
Bình luận (0)
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2widehat{BCF} + widehat{CFB} 90^{circ}$.
c. Gọi $M$ là giao điểm của hai đư...
Đọc tiếp
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC > BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2\widehat{BCF} + \widehat{CFB} = 90^{\circ}$.
c. Gọi $M$ là giao điểm của hai đường thẳng $BD$ và $CH$. Chứng minh hai đường thẳng $EM$ và $AB$ song song với nhau.
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
Cho hình thang ABCD có AB // CD và AB < CD. Gọi O là giao điểm của hai
đường chéo, I là giao điểm của hai đường thẳng chứa hai cạnh bên; M và N thứ tự là
trung điểm của hai đáy AB và CD. Chứng minh rằng 4 điểm O, I, M, N thẳng hàng.
cho hình thang cân ABCD có ab//cd gọi o là giao điểm của 2 đường chéo gọi E là giao điểm của 2 đường thẳng chứa 2 cạnh bên . chứng minh rằng chứng minh EO là đường trung trực của AB
Để chứng minh rằng EO là đường trung trực của AB trong hình thang cân ABCD, ta cần sử dụng một số kiến thức về hình học và các định lý liên quan.
Đầu tiên, do hình thang ABCD là hình thang cân, ta có AB // CD. Điều này có nghĩa là tam giác ABE và CDE là hai tam giác đồng dạng (có các cặp góc tương đồng và các cặp cạnh tương tỉ).
Tiếp theo, ta biết rằng đường chéo AC của hình thang cân là đường trung tuyến, có nghĩa là nó chia đôi đường chéo BD. Do đó, ta có AO = OC và BO = OD.
Giả sử EO không phải là đường trung trực của AB. Khi đó, ta có hai trường hợp xảy ra:
Trường hợp 1: EO nằm bên trong tam giác ABE. Trong trường hợp này, ta có EO cắt AB tại một điểm F. Vì tam giác ABE và CDE đồng dạng, nên ta cũng có EF // CD. Tuy nhiên, điều này mâu thuẫn với giả thiết AB // CD. Vậy trường hợp này không xảy ra.
Trường hợp 2: EO nằm bên ngoài tam giác ABE. Trong trường hợp này, ta có EO cắt AB tại một điểm F. Vì tam giác ABE và CDE đồng dạng, nên ta cũng có EF // CD. Tuy nhiên, điều này cũng mâu thuẫn với giả thiết AB // CD. Vậy trường hợp này cũng không xảy ra.
Vì hai trường hợp trên không xảy ra, ta kết luận rằng EO phải là đường trung trực của AB trong hình thang cân ABCD.
Hy vọng rằng giải thích trên đã giúp bạn hiểu và chứng minh được rằng EO là đường trung trực của AB trong hình thang cân ABCD.
Đúng 0
Bình luận (0)
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
mà OA=OB
nên EO là trung trực của AB
Đúng 0
Bình luận (0)
cho hình thang cân ABCD có ab//cd gọi o là giao điểm của 2 đường chéo gọi E là giao điểm của 2 đường thẳng chứa 2 cạnh bên . chứng minh rằng chứng minh eo là đường trung trực của AB
Để chứng minh rằng EO là đường trung trực của AB trong hình thang cân ABCD, chúng ta có thể sử dụng các điều kiện và tính chất của hình thang cân.
Vì hình thang ABCD là hình thang cân, nên ta có ab//cd và AD = BC.
Điều này cho phép chúng ta sử dụng các tính chất của các tam giác đồng dạng để chứng minh EO là đường trung trực của AB.
Ta có thể chứng minh rằng tam giác AEO và tam giác BEO đồng dạng bằng cách sử dụng góc và cạnh tương đồng.
Từ ab//cd, ta có: ∠AEO = ∠BEO (góc đối) ∠EAO = ∠EBO (góc đối)
Vì AD = BC, ta có: AE/BE = AD/BC = AO/BO (điều này được gọi là tỉ số phân giác)
Từ đó, ta có thể kết luận rằng tam giác AEO và tam giác BEO đồng dạng (góc và cạnh tương đồng).
Do đó, theo tính chất của các tam giác đồng dạng, ta biết rằng EO là đường trung trực của AB.
Vậy, ta đã chứng minh được rằng EO là đường trung trực của AB trong hình thang cân ABCD.
Đúng 0
Bình luận (0)
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
mà OA=OB
nên EO là trung trực của AB
Đúng 0
Bình luận (0)
Cho hình thang ABCD có hai đáy là AB và CD. Gọi M là trung điểm của CD, E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh EF // AB
b) Đường thẳng EF cắt AD, BC lần lượt tại H và N. Chứng minh HE = EF = FN.
c) Biết AB = 7,5 cm, CD = 12 cm. Tính độ dài HN.
- Hình vẽ:
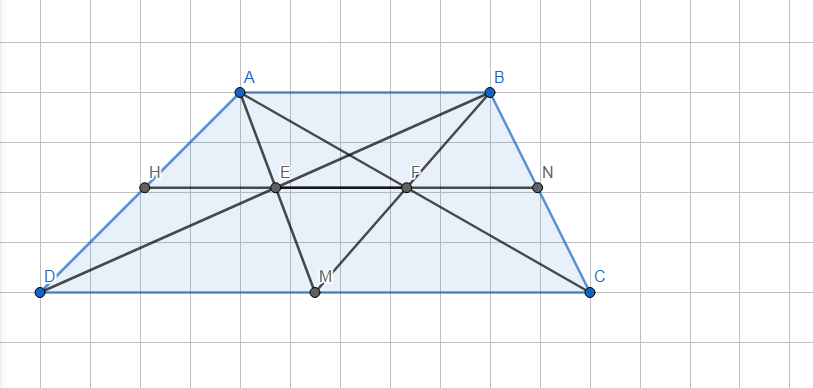
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).
Đúng 1
Bình luận (0)
Cho hình thang ABCD
(
A
B
/
/
C
D
)
.
Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O và song song với hai đáy cắt AD tại E. Biết
A
B
4
c
m
,
C
D
6
c
m
.
Tỉ số đồng dạng của hai tam giác AOE và ACD là: A.
2
3
B....
Đọc tiếp
Cho hình thang ABCD ( A B / / C D ) . Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O và song song với hai đáy cắt AD tại E. Biết A B = 4 c m , C D = 6 c m . Tỉ số đồng dạng của hai tam giác AOE và ACD là:
A. 2 3
B. 12 5
C. 2 5
D. 4 5




















