Bài 1 : Tìm u và v biết rằng u -v = 2010; u + v = 2011
Bài 2 : Tìm nghiệm tổng quát của phương trình 17x + 7y = 2007
Bài 3 : Cho tam giác ABC có góc A vuông và AB = AC. Đường cao hạ từ A xuống BC bằng 4cm. Hãy tính độ dài các cạnh của tam giác ABC
Tìm u và v biết rằng u - v = 2010 ; u + v = 2011
Ta có : u-v = 2010
\(\Leftrightarrow\)u=2010+v (1)
Thay (1) vào u+v=2011 ta có :
u+v=2011
\(\Leftrightarrow\)2010+v+v=2011
\(\Leftrightarrow\)2v=1
\(\Leftrightarrow\)v=\(\frac{1}{2}\)=0,5
\(\Rightarrow\)u=\(0,5+2010=2010,5\)
Vậy \(\left\{{}\begin{matrix}u=2010,5\\v=0,5\end{matrix}\right.\)
Tìm u – v biết rằng u + v = 15, uv = 36 và u > v
A. 8
B.12
C. 9
D. 10
Ta có S = u + v = 15, P = uv = 36. Nhận thấy S 2 = 225 > 144 = 4P nên u, v là hai nghiệm của phương trình
x 2 – 15x + 36 = 0 ⇔ (x – 12)(x – 3) = 0 ⇔ x = 12 x = 3
Vậy u = 12; v = 3 (vì u > v) nên u – v = 12 – 3 = 9
Đáp án: C
Tìm u – 2v biết rằng u + v = 14, uv = 40 và u < v
A. −6
B. 16
C. −16
D. 6
Ta có S = u + v = 14, P = uv = 40. Nhận thấy S 2 = 196 > 160 = 4P nên u, v là hai nghiệm của phương trình x 2 – 14x + 40 = 0 ⇔ (x – 4)(x – 10) = 0
⇔ x = 4 x = 10
Vậy u = 4; v = 10 (vì u < v) nên u – 2v = 4 – 2.10 = −16
Đáp án: C
Bài 1: Cần dùng bao nhiêu chữ số để đánh số trang của một quyển sách có 126 trang ?
Bài 2:Tìm 4 số tự nhiên liên tiếp ,biết rằng tổng của chúng = 2010
Bài 1 giải
Từ trang 1 đến trang 9 có số trang là :
9 - 1 +1 = 9 ( trang )
Từ trang 1 đến trang 9 cần số chữ số là :
9 x 1 =9 ( chữ số )
Từ trang 10 đến trang 99 cần số trang là :
99 - 10 + 1 = 90 ( trang )
Từ trang 10 đến trang 99 cần số chữ số là :
90 x 2 = 180 (chữ số )
Sang trang phải đánh 3 chữ số là :
126 - 9 - 90 = 27 ( trang )
Số chữ số để đánh 27 trang là :
27 x 3= 81 ( chữ sô )
Số chữ số để đánh số trang sách dày 126 trang là :
9 + 180 + 81 = 270 (chữ số )
Đấp số: 270 chữ số
Bài 2
Trung bình cộng của 4 số là :
2010 : 4 = 502
Số 502 là số trung bình cộng của 4 số hay cũng là số thứ 2
Số thứ nhất :
502 -1 =501
Số thứ ba :
502+1=503
Số thứ 4 :
503 +1 = 504
Đáp sô :.....
b1: can 270 chu so
b2 : 501;502;503;504
Tìm hai số u và v biết: u +v =1, uv =- 42 và u >v .
\(u+v=1\Rightarrow v=1-u\)
Thế vào \(uv=-42\Rightarrow u\left(1-u\right)=-42\)
\(\Rightarrow u^2-u-42=0\Rightarrow\left[{}\begin{matrix}u=7\Rightarrow v=-6\\u=-6\Rightarrow v=7>u\left(loại\right)\end{matrix}\right.\)
Giả sử rằng u, v và w là các số nguyên dương sao cho:
\(u+\frac{1}{v+\frac{1}{w+1}}=\frac{23}{7}\)
Tìm u, v và w, và giải thích tại sao giá trị bạn tìm được là giá trị duy nhất tìm được.
\(\frac{23}{7}=3+\frac{1}{3+\frac{1}{2}}=3+\frac{1}{3+\frac{1}{1+1}}\)
Trong không gian với hệ tọa độ Oxyz, biết u → = 2 ; v → = 1 ; và góc giữa hai vectơ u → và v → bằng 2 π 3 . Tìm k để vectơ p → = k u → + v → vuông góc với vectơ q → = u → - v → .
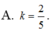
![]()
![]()
![]()
tìm u và v biết u+2=4 và u^(2)+v^(2)= 65
Tìm hai số u và v biết: u +v =1, uv =- 42 và u >v .