b) Xét phương trình 2 có 
(1-x² )/(1+xy)² - (x+y)²    - y² =1
=>(1-x²)/1+2xy+x²y²-x²-2xy-y²   -y²=1
=>(1-x²) /(1-x² )-y²(1-x²)       -y² =1
=>(1-x²)/(1-x²)(1-y²)       -y²=1
=>1/(1-y²)    -y²=1
=>1=(1-y²)²
=>1=1-2y²+y4
=>y⁴-2y²=0
=>y²(y²-2)=0
=>y=0
y²-2=0
=> y=+√2
=> y=-√2
 Thay y vào phương trình 1 là ra x 

à nhầm ... sửa lại dòng 6 
=> 1/(1-y²) - y²=1
=> 1/(1-y²)=1+y²
=> 1=1-y⁴
=> y=0
=>x=3
=> x=-3
 

Đặt \(\begin{cases}S=x+y\\P=xy\end{cases}\) hpt đầu trở thành:

\(\begin{cases}S^2-P=9\\S+P=3\end{cases}\)\(\Leftrightarrow\begin{cases}S^2-P=9\\S=3-P\end{cases}\)

\(\Leftrightarrow\left(P-3\right)^2-P=9\)\(\Leftrightarrow P^2-7P+9-9=0\)

\(\Leftrightarrow P\left(P-7\right)=0\Leftrightarrow\)\(\left[\begin{array}{nghiempt}P=0\\P=7\end{array}\right.\)

Suy ra hệ đầu tương đương \(\begin{cases}x+y=3\\xy=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=3\\y=0\end{cases}\) hoặc \(\begin{cases}x=0\\y=3\end{cases}\)

Suy ra hệ đầu tương đương \(\begin{cases}x+y=-4\\xy=7\end{cases}\) giải ra ta dc vô nghiệm

Vậy hệ pt trên có nghiệm (x;y) thỏa mãn là (3;0) và (0;3)

đối xứng loại 1 đặt ẩn bình lm j =))

1 số gợi ý

hpt \(\Leftrightarrow\left\{{}\begin{matrix}2x\left(2x-2y-1\right)=6\left(y+2\right)\\6y+12\sqrt{2x-1}=2y^2-2x+46\end{matrix}\right.\)(1)

Đặt \(\sqrt{2x-1}=t\left(t\ge0\right)\)

(1)\(\Leftrightarrow\left\{{}\begin{matrix}\left(t^2+1\right)\left(t^2-2y\right)=6\left(y+2\right)\left(2\right)\\6y+12t=2y^2-t^2+45\end{matrix}\right.\)

(2)\(\Leftrightarrow\left(t^2+4\right)\left(t^2-2y-3\right)=0\)

\(\Leftrightarrow t^2-2y-3=0\)

ta có hpt mới sau : \(\left\{{}\begin{matrix}t^2-2y-3=0\\2y^2-t^2+45=6y+12t\end{matrix}\right.\)

một cách trâu bò nhưng hiệu quả là

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{t^2-3}{2}\\2y^2-t^2-6y-12t+45=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{t^2-3}{2}\\2\left(\dfrac{t^2-3}{2}\right)^2-t^2-6\left(\dfrac{t^2-3}{2}\right)-12t+45=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{t^2-3}{2}\\t=3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\t=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=5\end{matrix}\right.\)

\(\left(a,b,n\in N\right)\left\{{}\begin{matrix}n^2=a+b\\n^3+2=a^2+b^2\end{matrix}\right.\)

Áp dụng BĐT cơ bản : \(x^2+y^2\ge\dfrac{1}{2}\left(x+y\right)^2\)

\(\rightarrow n^3+2=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2=\dfrac{1}{2}\left(n^2\right)^2=\dfrac{1}{2}n^4\)

\(\Rightarrow n^3+2-\dfrac{n^4}{2}\ge0\)\(\Rightarrow0\le n\le2\)

Xét từng TH của n và kết quả nhận được là \(n=2\); (a,b) là hoán vị của (1,3)

tớ mượn test cái nha

Áp dụng định lí viet ta có :

\(\left\{{}\begin{matrix}x_1+x_2=-3\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)

\(x_1\left(x_1^4-1\right)+x_2\left(32x_2^4-1\right)=3\)

\(\leftrightarrow\left(x_1\right)^5+\left(2x_2\right)^5-\left(x_1+x_2\right)=3\)

\(\leftrightarrow x_1^5+\left(2x_2\right)^5-\left(-3\right)=3\)

\(x_1^5+\left(2x_2\right)^5=0\leftrightarrow x_1=-2x_2\)

Thay vào (1)\(\rightarrow x_1=-6;x_2=3\)

Thay vào (2)\(\rightarrow m-1=\left(-6\right).3=-18\rightarrow m=-17\)

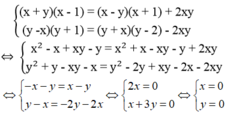
Vậy nghiệm của hệ phương trình là (x; y) = (0; 0)