Cho tam giác ABC cân tại A có AB = AC = 10cm; BC =12cm. Kẻ AH vuông góc với BC ( H thuộc BC)
a/ C/m: tam giác AHB = tam giác AHC
b/ Tính độ dài đoạn thẳng AH
c/Kẻ các đường trung tuyến BD, CE trong tam giác ABC . C/m BD +CE >18cm
Những câu hỏi liên quan
Cho tam giác ABC cân tại A có AB AC 13cm; BC 10cm. Tính sin A A. sin A
120
169
B. sin A
60
169
C. sin A
5
6
D. sin A
10
13
Đọc tiếp
Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A
A. sin A = 120 169
B. sin A = 60 169
C. sin A = 5 6
D. sin A = 10 13
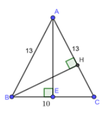
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
Mặt khác:
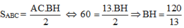
Xét ABH vuông tại H có:
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB = AC =13cm ; BC =10cm. Tính cos A
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg
Xem chi tiết
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 1
Bình luận (0)
cho tam giác abc cân tại a có ab=10cm ,bac=30 tính bán kính đường tròn tiếp xúc với ab và ac tại b ,c
Cho tam giác abc vuông tại a có ab bằng 6cm bc bằng 10cm a tính ac b trên tia đối của tia ab lấy điểm d sao cho ad bằng ab chứng minh Tam giác abc bằng tam giác adc c đường thẳng qua a song song với bc cắt CD tại E chứng minh Tam giác EAC cân
a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
Đúng 2
Bình luận (1)
Cho tam giác ABC cân tại A, có AB=6cm, BC=10cm .Vẽ đường phân giác BD (D thuộc cạnh AC).Tính độ dài các đoạn AD và DC
\(AC=AB=6\)
Áp dụng định lý phân giác:
\(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{AD}{6}=\dfrac{6-AD}{10}\)
\(\Leftrightarrow10AD=36-6AD\Rightarrow AD=\dfrac{9}{4}\) (cm)
\(\Rightarrow DC=AC-AD=\dfrac{15}{4}\) (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Vẽ trung tuyến AM của tam giác. Biết B C = 12 c m , A B = A C = 10 c m thì độ dài AM là:
A. 22cm
B. 4cm
C. 8cm
D. 10cm
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A có A B = A C = 10 c m , đường trung tuyến AM (M∈BC) có độ dài là 6cm. Khi đó BC có độ dài là:
A. 16cm
B. 12cm
C. 14cm
D. 8cm
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pytago trong tam giác vuông ABM có:
BM^2=AB^2-AM^2=10^2-6^2=64=>AM=8cm. Chọn D
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có A B = A C = 10 c m , đường trung tuyến AM (M∈BC) có độ dài là 6cm. Khi đó BC có độ dài là:
A. 16cm
B. 12cm
C. 14cm
D. 8cm
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pytago trong tam giác vuông ABM có:
BM^2=AB^2-AM^2=10^2-6^2=64=>AM=8cm.
Chọn D
Đúng 0
Bình luận (0)