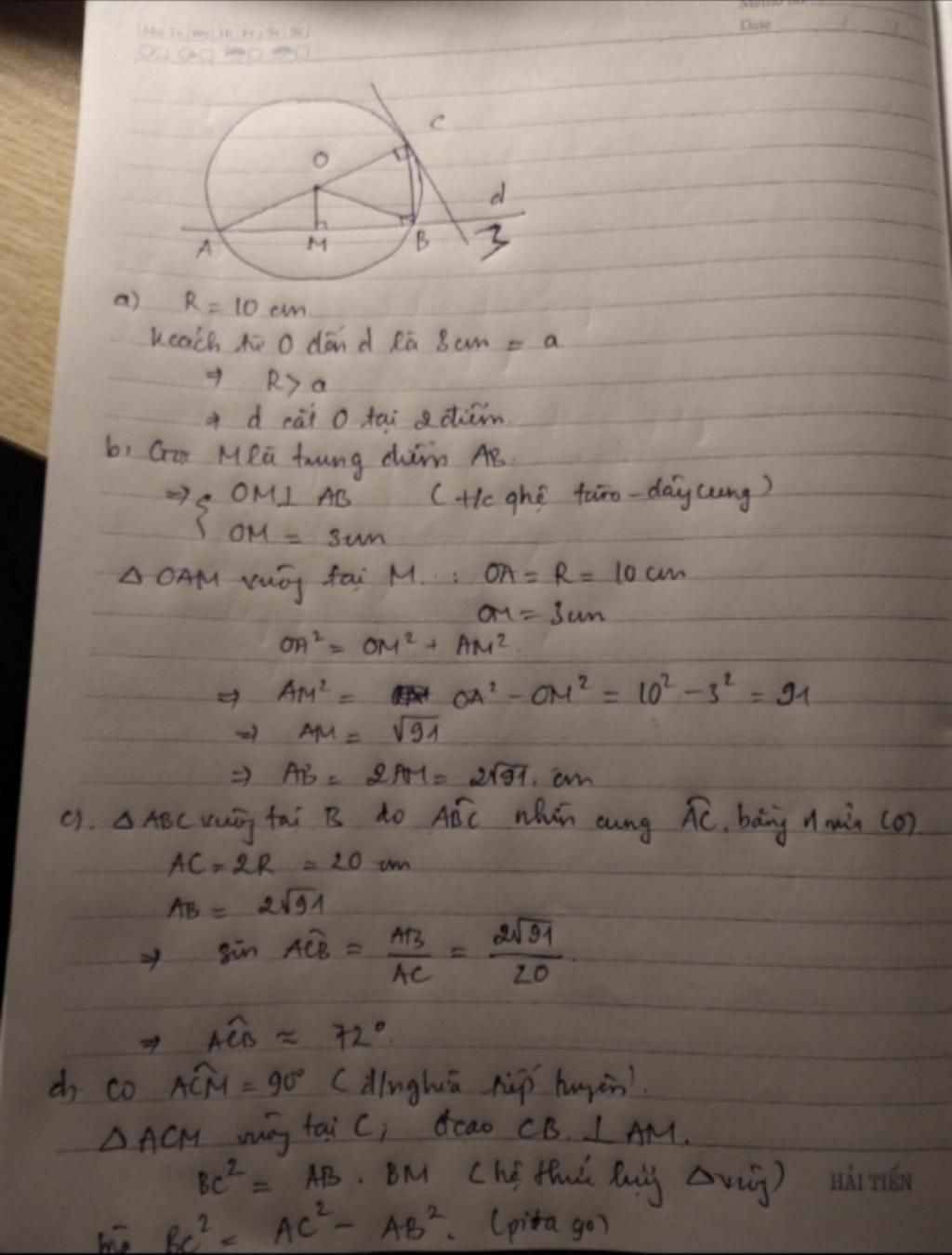Từ điểm A nằm ngoài đtron (O;2cm). Kẻ hai tiếp tuyến AB, AC và cát tuyến AMN với đường tròn đó ( M nằm giữa N và A) cho góc BAC có số đo bằng 60 độ
a) chứng minh tứ giác ABOC nội tiếp đường tronfd. xác định tâm và bán kính đường tròn ngoại tiếp tứ giác ABOC
b) CM : AB2= AN.AM
c) tính diện tích phần giới hạn bởi các đoạn AB, AC và cung nhỏ BC nói trên

Những câu hỏi liên quan
Từ điểm A nằm ngoài đường tròn (O,R), kẻ 2 tiếp tuyến AB,AC (B,C tiếp điểm) a) Cmr 4 điểm A,B,O,C cùng thuộc 1 đtron b)cmr BC<AO
Xét (O; R):
AB là tiếp tuyến; B là tiếp điểm (gt).
=> OB vuông góc AB (Tính chất tiếp tuyến).
=> Tam giác ABO vuông tại B.
=> A; B; O thuộc đường tròn đường kính OA. (1)
Xét (O; R):
AC là tiếp tuyến; C là tiếp điểm (gt).
=> OC vuông góc AC (Tính chất tiếp tuyến).
=> Tam giác ACO vuông tại C.
=> A; C; O thuộc đường trong đường kính AO. (2)
Từ (1); (2) => A; B; O; C cùng thuộc đường tròn đường kính AO (đpcm).
Đúng 0
Bình luận (0)
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
từ điểm A nằm ngoài đt (O) kẻ tiếp tuyến AB,AC. Đường thẳng qua cắt (O) tại D;E (D nằm giữa A và E). M là trung điểm AC, BM cắt (O) tại N (N≠B). K là tâm đtron ngoại tiếp tam giác ANC. Cm: CK vuông góc với BC.
bài cho mng tham khảo ạ
góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
góc A chung
góc NBD=góc AEB
=>ΔABD đồng dạg vơi ΔAEB
=>AB/AE=AD/AB=BD/EB
Chứng minh tương tự, ta được: ΔACD đồng dạng với ΔAEC
=>AC/AE=CD/CE
mà AB=AC
nên AD/AB=AD/AC
=>BD/BE=CD/CE
=>BD*CE=BE*CD
góc M chung
góc MCN=góc MBC
=>ΔMCN đồng dạng với ΔMBC
=>MC/MB=MN/MC
=>MB*MN=MC^2=MA^2
=>MA/MB=MN/MA
=>ΔMAN đồng dạng với ΔMBA
=>góc MAN=góc MBA
=>BC là tiếp tuyến của (K)
=>BC vuông góc CK
Đúng 0
Bình luận (0)
Cho(O,R) từ điểm A been ngoài đường trònker 2 tiếp tuyến AB,AC với đtron .Từ B kẻ đường thẳng song song với AC cắt đtron tại D . Nối AD cắt đtron (O) tại điểm thứ 3 là K .Nối BK cắt AC tại I
a cm ABOC nội tiếp
B, IC2 =IK .IB
c, Cho BAC= 60° CM A, O, D thẳng hàng
Từ điểm M nằm ngoài đường tròn O,R vẽ tiép tuyến MA,dây cung AB vuông góc với OM tại H Chứng minh H là tđiểm của AB và MB là tiếp tuyến của đường tròn O Vẽ đkinh BC của đtrofn ,Mc cắt đtron tại D,cắt AB tại I.c.minh MH.MO=MD.MC
a: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB và OH là phân giác của góc AOB
Xét ΔOAM và ΔOBM co
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiếp tuyến của (O)
b: Xet ΔMAD và ΔMCA có
góc MAD=góc MCA
góc AMD chung
Do đó: ΔMAD đồng dạng với ΔMCA
=>MA/MC=MD/MA
=>MA^2=MC*MD=MH*MO
Đúng 0
Bình luận (0)
qua M nằm ngoài đtron (O), vẽ 2 tiếp tuyến MA, MB (A, B là tiếp điểm). Trên cung nhỏ AB lấy E sao cho sđAE>sđBE. CD là đường vuông góc với OE tại E (C∈MA; D∈MB).
Chứng minh rằng \(\dfrac{MC}{OA}+\dfrac{MD}{OB}=\dfrac{CD}{OE}\)
giúp em vớiiiii, em cần gấp
Cho 2 đtron bằng nhau tâm O và O' cắt nhau tại A và B vẽ đường kính AC của đtron (O) và AD của đtron (O') Gọi E là giao điểm AC với đtron (OO')
a, So sánh cung BC và cung BD của 2 đtron
b,CM:B là điểm chính giữa cung EBD
c,CM:O'B vuông góc với DE
Cho (O) có tiếp tuyến là MA MB( A,B là tiếp điểm) đường thẳng MO cắt đtron tại C và D(C nằm giữa O và M)cm góc ADM=COB
Sửa đề: góc ADM=1/2*góc COB
Xét (O) có
MA,MB là tiếp tuyến
nên OM là phân giác của góc AOB
=>gócAOM=góc BOM
=>góc AOC=góc BOC
=>sđ cung AC=sđ cung BC
mà góc ADM=1/2*sđ cung AC
nên góc ADM=1/2*góc COB
Đúng 0
Bình luận (0)
Cho đtron đkinh 10cm, 1 đường thẳng d cách tâm O 1 khoảng 3cm.a, Xác định vtri tương đối của đường thẳng d và đtron (O)b, Đường thẳng d cắt đtron (O) tại điểm A và B. Tính độ dài dây ABc, Kẻ đường kính AC của đtron (O). Tính độ dài BC và số đo widehat{CAB} (làm tròn đến độ)d, Tiếp tuyến của đtron (O) tại C cắt tia AB tại M. Tính độ dài BM
Đọc tiếp
Cho đtron đkinh 10cm, 1 đường thẳng d cách tâm O 1 khoảng = 3cm.
a, Xác định vtri tương đối của đường thẳng d và đtron (O)
b, Đường thẳng d cắt đtron (O) tại điểm A và B. Tính độ dài dây AB
c, Kẻ đường kính AC của đtron (O). Tính độ dài BC và số đo \(\widehat{CAB}\) (làm tròn đến độ)
d, Tiếp tuyến của đtron (O) tại C cắt tia AB tại M. Tính độ dài BM
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Đọc tiếp
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AOa) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.b) Cho AB 8cm;BC 9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE góc BDE.
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AO
a) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.
b) Cho AB = 8cm;BC =9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)
c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE = góc BDE.
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)
Đúng 0
Bình luận (0)