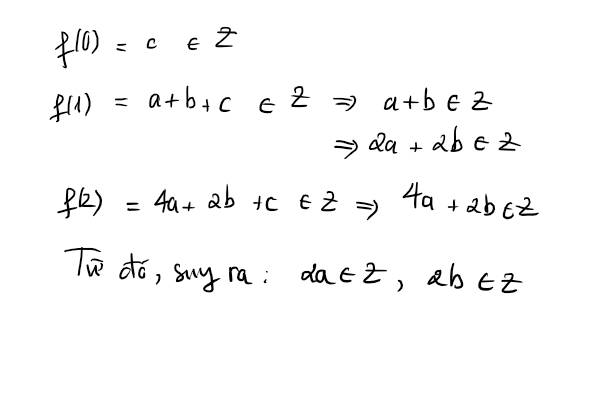cho f(x) = ax^2 + bx +c biết 2a+b = 0 . chưng s minh f(-1) * f(3) >=0

Những câu hỏi liên quan
a
cho f(x) = \(ax^2+bx+c\) ( a ; b ; c ∈Q )
Biết f(0) ; f(1) ; f(2) có giá trị nguyên.
chứng minh rằng 2a , 2b có giá trị nguyên
Lời giải:
$f(0)=a.0^2+b.0+c=c$ nguyên
$f(1)=a+b+c$ nguyên, mà $c$ nguyên nên $a+b+c-c=a+b$ nguyên
$f(2)=4a+2b+c=2a+2(a+b)+c$ nguyên mà $a+b, c$ nguyên nên $2a$ nguyên
$2a$ nguyên, $2(a+b)$ nguyên nên $2b$ nguyên.
Ta có đpcm.
Đúng 2
Bình luận (0)
cho đa thức f(x)=ax^2+bx+c với a,b,c là các số thực. biết f(0),f(1),f(2) có giá trị nguyên. chứng minh 2a,2b có giá trị nguyên
Ta có:
\(f\left(0\right)=c\in Z\)(1)
\(f\left(1\right)=a+b+c\in Z\)(2)
\(f\left(2\right)=4a+2b+c\in Z\)(3)_
Từ (1), (2) => \(a+b\in Z\)=> \(2a+2b\in Z\)(4)
Từ (1), (3)=> 4a+2b\(\in Z\)(5)
Từ (4), (5) => \(\left(4a+2b\right)-\left(2a+2b\right)\in Z\)
=> \(2a\in Z\)=> \(2b\in Z\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
cho đa thức f(x) = ax2 + bx +c với a,b,c là các số thực .Biết rằng f(0) ; f(1) ; f(2) có giá trị nguyên . Chứng minh rằng 2a, 2b có giá trị nguyên
\(f\left(0\right)=a.0^2+b.0+c=c\) có giá trị nguyên
\(f\left(1\right)=a+b+c\) có giá trị nguyên => a + b có giá trị nguyên
\(f\left(2\right)=4a+2b+c=2a+2\left(a+b\right)+c\)=> 2a có giá trị nguyên
=> 4a có giá trị nguyên
=> 2b có giá trị nguyên.
cho f(x)=ax^2+bx+c biết bc^2a^4 > 0. Xác định dấu của f(-1) - f(1)
Cho hàm số f(x) = ax2 + bx - 2a/3 (a khác 0)
Chứng minh rằng f(1), f(-1), f(0) không thể cùng dấu
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+6b+19c=0
CMR: phương trình ax^2 + bx +c = 0 có nhiệm trong đoạn [0;1/3]
--------
ta có:
f(0) = c
f(1/3) = a/9 + b/3 + c
=> f(0) + 18.f(1/3) = c + 2a + 6b + 18c = 2a + 6b + 19c = 0 (*)
Nếu f(0) = 0 hoặc f(1/3) = 0 => f(x) = 0 có nghiệm là 0 hoặc 1/3 thuộc [0,1/3]
nếu f(0) ≠ 0 và f(1/3) ≠ 0 tự (*) => f(0).f(1/3) ≤ 0 => f(x) = 0 có nghiệm thuộc [0,1/3]
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+3b+6c=0
a) Tính a,b,c theo f(0), f(1), f(1/2)
f(0) = c
f(1) = a + b + c
f(1/2) = a/4 + b/2 + c
b) CMR ba số f(0), f(1), f(1/2) không thể cùng dấu:
f(0) + f(1) + 4f(1/2) = c + a+b+c + a + 2b + 4c = 2a + 3b + 6c = 0
=> f(0) , f(1) , f(1/2) không thể cùng dấu.
Đúng 0
Bình luận (0)
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+6b+19c=0
CMR: phương trình ax^2 + bx +c = 0 có nhiệm trong đoạn [0;1/3]
--------
ta có:
f(0) = c
f(1/3) = a/9 + b/3 + c
=> f(0) + 18.f(1/3) = c + 2a + 6b + 18c = 2a + 6b + 19c = 0 (*)
Nếu f(0) = 0 hoặc f(1/3) = 0 => f(x) = 0 có nghiệm là 0 hoặc 1/3 thuộc [0,1/3]
nếu f(0) ≠ 0 và f(1/3) ≠ 0 tự (*) => f(0).f(1/3) ≤ 0 => f(x) = 0 có nghiệm thuộc [0,1/3]
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+3b+6c=0
a) Tính a,b,c theo f(0), f(1), f(1/2)
f(0) = c
f(1) = a + b + c
f(1/2) = a/4 + b/2 + c
b) CMR ba số f(0), f(1), f(1/2) không thể cùng dấu:
f(0) + f(1) + 4f(1/2) = c + a+b+c + a + 2b + 4c = 2a + 3b + 6c = 0
=> f(0) , f(1) , f(1/2) không thể cùng dấu.
:3
Đúng 0
Bình luận (0)
ta có:
f(0) = c
f(1/3) = a/9 + b/3 + c
=> f(0) + 18.f(1/3) = c + 2a + 6b + 18c = 2a + 6b + 19c = 0 (*)
Nếu f(0) = 0 hoặc f(1/3) = 0 => f(x) = 0 có nghiệm là 0 hoặc 1/3 thuộc [0,1/3]
nếu f(0) ≠ 0 và f(1/3) ≠ 0 tự (*) => f(0).f(1/3) ≤ 0 => f(x) = 0 có nghiệm thuộc [0,1/3]
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+3b+6c=0
a) Tính a,b,c theo f(0), f(1), f(1/2)
f(0) = c
f(1) = a + b + c
f(1/2) = a/4 + b/2 + c
b) CMR ba số f(0), f(1), f(1/2) không thể cùng dấu:
f(0) + f(1) + 4f(1/2) = c + a+b+c + a + 2b + 4c = 2a + 3b + 6c = 0
=> f(0) , f(1) , f(1/2) không thể cùng dấu.
Đúng 0
Bình luận (0)
F(x)= ax+b ;a khác 0
biết F(1)= 0 ; F(2)= 4
G(x)= ax^2+bx+c ;a khác 0
biết G(1) = 0; G(-1)= 9 ; G(2)= 5
cho đa thức f(x)= ax^2+bx+ca khác 0
biết f(1)= f(-1)
CM :f(x)= f(-x)
no hiểu gì hết THIS IS HOW I DO NOT KNOW HOW TO APOLOGIZE OFFLINE
Đúng 0
Bình luận (3)
Cho đa thức:f(x)=\(ax^2\)+bx+c với a,b,c là các số thực.Biết f(0),f(1),f(2) có giá trị nguyên.Chứng minh 2a,2b có giá trị nguyên
Cho đa thức: f(x)= ax^2+bx=c. Biết 13a+b+2c= 0. Chứng minh f(-2).f(3) > hoặc = 0