cho hàm số y=\(x^2\) có đò thị là (P).Đt y=b cắt (P) tại hai điểm A,B, tìm b để\(\Delta OAB\) đều

Những câu hỏi liên quan
cho hs y= (m-2)x+m+3. tìm m để
a; đồ thị hàm số // đt y= x+3
b; đths cắt đt y=2x+4 tại điểm có tung độ =4
a) Khi dó thì m - 2 =1 và m + 3 ≠ 3 ⇨ m = 3 và m ≠ 0 => m = 3 thỏa mãn.
b) Khi đó x = 0 và y = 4 => m + 3 = 4 => m =1
Đúng 0
Bình luận (0)
1) vẽ đồ thị hàm số y=|x|
2) vẽ đường thẳng y=2 cắt đò thị hàm số trên tại 2 điểm A và B. tính chu vi tam giác OAB
Cho hàm số \(y=\frac{3x+4}{3x+3}\) có đồ thị (C). Tìm các giá trị tham số m để đường thẳng d : y = x + m cắt đồ thị (C) tại hai điểm phân biệt A và B sao cho tam giác OAB đều ( với O là gốc tọa độ)
Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4
Đúng 0
Bình luận (0)
cho hàm số bậc nhất y=(m-1)x+4 có đồ thị là đường thẳng d tìm m để đường thẳng d cắt trục ox ,oy lần lượt tại hai điểm A,B sao cho diện tích tam giác OAB bằng 2
Xem chi tiết
2) cho hàm số yleft(a-1right)x+a left(ane1right) (1)a) chứng tỏ: đò thị hàm số (1) luôn đi qua (-1; 1)b) xác định a để đồ thị (1) cắt trục tung tại điểm có tung độ 3. vẽ đồ thị hàm sốc) xác định a để đò thị (1) cắt trục hoành tại điểm có hoành độ -2. tính khoảng cách từ gốc tọa độ O tới đường thẳnggiúp mk vs ah mk cần gấp
Đọc tiếp
2) cho hàm số \(y=\left(a-1\right)x+a\) \(\left(a\ne1\right)\) (1)
a) chứng tỏ: đò thị hàm số (1) luôn đi qua (-1; 1)
b) xác định a để đồ thị (1) cắt trục tung tại điểm có tung độ 3. vẽ đồ thị hàm số
c) xác định a để đò thị (1) cắt trục hoành tại điểm có hoành độ -2. tính khoảng cách từ gốc tọa độ O tới đường thẳng
giúp mk vs ah mk cần gấp
a, gọi điểm hàm số (1) luôn đi qua là A(xo,yo) thì xo,yo thỏa mãn (1)
\(=>yo=\left(a-1\right)xo+a< ->a.\left(xo+1\right)-\left(xo+yo\right)=0\)
\(=>\left\{{}\begin{matrix}xo+1=0\\xo+yo=0\end{matrix}\right.\)=>xo=-1,yo=1 vậy.....
b,\(=>x=0,y=3=>\left(1\right):a=3\)(tm)
c,\(=>x=-2,y=0=>\left(1\right):0=\left(a-1\right)\left(-2\right)+a=>a=2\left(tm\right)\)
\(=>y=x+2\) cho x=0=>y=2=>A(0;2)
cho y=0=>x=-2=>B(-2;0)
gọi OH là khoảng cách từ gốc tọa độ đến đồ thị hàm số(1)
\(=>\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=>\dfrac{1}{OH^2}=\dfrac{1}{2^2}+\dfrac{1}{\left(-2\right)^2}=>OH=....\)
Đúng 1
Bình luận (0)
Cho hàm số y= - x2 có đồ thị (P) . Gọi d là đt đi qua điểm M ( 0;1) và có hệ số góc là k
a. Viết pt đuong thẳng d
b. Tìm điều kiện của k để đường thẳng d cắt đồ thị (P) tại hai điểm phân biệt
Lời giải:
Gọi đường thẳng (d)(d) có dạng y=kx+by=kx+b. Vì I(0;1)∈(d)⇒b=1⇒(d):y=kx+1I(0;1)∈(d)⇒b=1⇒(d):y=kx+1
Phương trình hoành độ giao điểm x2+kx+1=0x2+kx+1=0.
Theo đó, nếu A,B=(d)∩(P)A,B=(d)∩(P) thì áp dụng hệ thức Viet ta có: x1+x2=−kx1+x2=−k
Trung điểm của ABAB là II nằm trên trục trung khi 0=xI=x1+x22=−k2⇒k=00=xI=x1+x22=−k2⇒k=0
Do đó k=0k=0 là kết quả cần tìm.
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
y
2
x
x
−
2
cắt đường thẳng
y
x
+
m
tại hai điểm phân biệt A,B sao cho tam giác OAB nhận
G
1
;
5
3
làm trọng tâm. A. m3 B. m4 C...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = 2 x x − 2 cắt đường thẳng y = x + m tại hai điểm phân biệt A,B sao cho tam giác OAB nhận G 1 ; 5 3 làm trọng tâm.
A. m=3
B. m=4
C. m=1
D. m=7
Đáp án C
Điều kiện: x≠2.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình
2 x x − 2 = x + m ⇔ 2 x x − 2 − x − m = 0 ⇔ 2 x − x 2 + 2 x − m x + 2 m x − 4 = 0 ⇔ − x 2 + 4 − m x + 2 m x − 2 = 0.
Để hai đồ thị hàm số giao nhau tại hai điểm phân biệt A,B ta có
4 − m 2 + 8 m > 0 g 2 ≠ 0 ⇔ m 2 + 16 > 0 − 4 + 8 − 2 m + 2 m ≠ 0
thỏa mãn với mọi m ∈ ℝ .
Theo bài ra ta có x A + x B + x O = 3 x A + m + x B + m + y O = 7 ⇔ 4 − m = 3 4 − m + 2 m = 5 ⇔ m = 1 .
Vậy m=1 thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Cho đồ thị hàm số y=(2m+1)x -m+3
a) Xác định m để cắt Ox, Oy tại A, B sao cho diện tích tam giác OAB=2
b) TÌm điểm cố định để đồ thị hàm số luôn đi qua với mọi m.
Cho hàm số
y
x
+
1
x
-
2
. Số các giá trị tham số m để đường thẳng yx+m luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn
x
2...
Đọc tiếp
Cho hàm số y = x + 1 x - 2 . Số các giá trị tham số m để đường thẳng y=x+m luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn x 2 + y 2 - 3 y = 4 là
A.1
B.0
C.3
D.2
Chọn D
Phương trình hoành độ giao điểm :
![]()
Theo yêu cầu bài toán : ![]() phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác ![]()
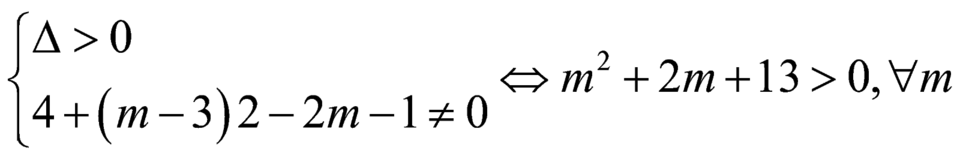
Gọi ![]() ,
,![]() suy ra
suy ra ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() :
:
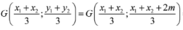
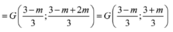
Theo yêu cầu bài toán :
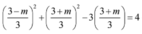
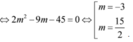 .
.
Đúng 0
Bình luận (0)
















