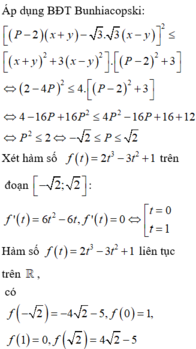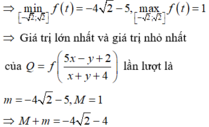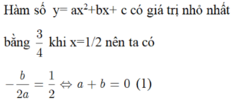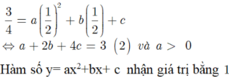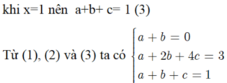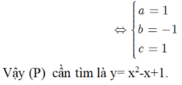hàm số y = \(|1-x|+|2x+4|\) có giá trị nhỏ nhất bằng

Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
x
-
m
2
x
+
4
với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1 A. m 2 B. m 0 C.
m
6
D. m 3
Đọc tiếp
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho các số thực x, y thay đổi thỏa mãn
x
2
+
y
2
-
x
y
1
và hàm số
f
t
2
t
3
-
3
t
2
-
1
. Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
Q
f...
Đọc tiếp
Cho các số thực x, y thay đổi thỏa mãn x 2 + y 2 - x y = 1 và hàm số f t = 2 t 3 - 3 t 2 - 1 . Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của Q = f 5 x - y + 2 x + y + 4 . Tổng M + m bằng
A. - 4 - 3 2
B. - 4 - 5 2
C. - 4 - 4 2
D. - 4 - 2 2
Cho hàm số y 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x
∈
[−3; 4] A.
max
−
3
;
4
y
4
B.
min
y
−
2
−
3...
Đọc tiếp
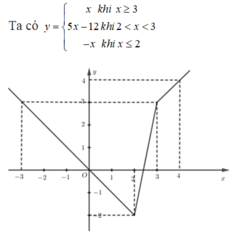
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Cho F(x) là một nguyên hàm của
f
(
x
)
2
x
+
1
trên R. Biết hàm số
y
F
(
x
)
đạt giá trị nhỏ nhất bằng
39
4
. Đồ thị của hàm số
y
F
(
x
)
cắt trục tung tại điểm có tung độ là A. 10 B. 11 C.
37
4
D.
39
4
Đọc tiếp
Cho F(x) là một nguyên hàm của f ( x ) = 2 x + 1 trên R. Biết hàm số y = F ( x ) đạt giá trị nhỏ nhất bằng 39 4 . Đồ thị của hàm số y = F ( x ) cắt trục tung tại điểm có tung độ là
A. 10
B. 11
C. 37 4
D. 39 4
Cho F(x) là một nguyên hàm của f(x) 2x + 1 trên R. Biết hàm số y F(x) đạt giá trị nhỏ nhất bằng
39
4
. Đồ thị của hàm số y F(x) cắt trục tung tại điểm có tung độ là A.
10
B.
11
C.
37
4
D.
39
4
Đọc tiếp
Cho F(x) là một nguyên hàm của f(x) = 2x + 1 trên R. Biết hàm số y = F(x) đạt giá trị nhỏ nhất bằng 39 4 . Đồ thị của hàm số y = F(x) cắt trục tung tại điểm có tung độ là
A. 10
B. 11
C. 37 4
D. 39 4
Xác định parabol (P) ; y ax2+bx+ c biết: Hàm số y ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x1/2 và nhận giá trị bằng khi x1. A. y x2+ x+1. B. y- x2-x+1. C. y -x2-x-1. D. y x2-x+1
Đọc tiếp
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
A. y= x2+ x+1.
B. y=- x2-x+1.
C. y= -x2-x-1.
D. y= x2-x+1
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
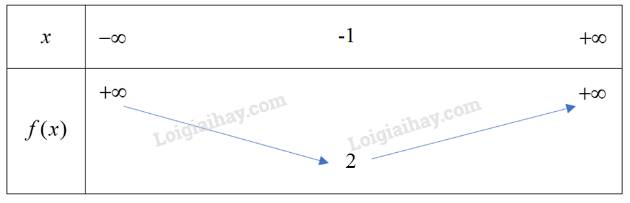
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị của tham số m để hàm số
y
2
m
x
+
m
2
+
m
-
2
x
+
m
có giá trị nhỏ nhất trên đoạn
1
;
4
bằng 1?...
Đọc tiếp
Có bao nhiêu giá trị của tham số m để hàm số y = 2 m x + m 2 + m - 2 x + m có giá trị nhỏ nhất trên đoạn 1 ; 4 bằng 1?
A. Vô số
B. 0
C. 2
D. 1
Chọn đáp án D
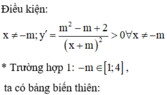
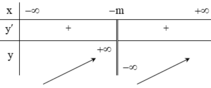


Vậy có đúng 1 giá trị của thỏa mãn điều kiện bài ra.

Đúng 0
Bình luận (0)
Giá trị nhỏ nhất của hàm số y = x 2 + 2 x (x>0)bằng
A. 4
B. 2
C. 1
D. 3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 1 - 8sin^2x cos^2x + 2 sin^4 2x
Đặt \(sin^24x=t\left(t\in\left[0;1\right]\right)\)
\(y=1-8sin^22x.cos^22x+2sin^42x\)
\(=1-2sin^24x+2sin^42x\)
\(\Rightarrow y=f\left(t\right)=1-2t+2t^2\)
\(y_{min}=min\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=\dfrac{1}{2}\)
\(y_{max}=max\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=1\)
Đúng 2
Bình luận (0)